【题目】如图,在平面直角坐标系中,矩形OABC的三个顶点A,O,C在坐标轴上,矩形的面积为12,对角线AC所在直线的解析式为y=kx-4k(k≠0).
(1)求A,C的坐标;
(2)若D为AC中点,过D的直线交y轴负半轴于E,交BC于F,且OE=1,求直线EF的解析式;
(3)在(2)的条件下,在坐标平面内是否存在一点G,使以C,D,F,G为顶点的四边形为平行四边形,若存在,请直接写出点G的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)A(4,0),B(0,3);(2)直线EF的解析式为y=![]() x-1;
x-1;
(3)存在;点G的坐标为(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).
【解析】
(1)设A(a,0),B(0,b),将A的坐标代入y=kx-4k(k≠0),解出a值,再根据矩形的面积为12,解出b即可;
(2)利用中点坐标公式求得点D的坐标,由点D和点E的坐标利用待定系数法求得直线EF的解析式即可;
(3)分别以DC、DF;CD、CF;CF、DF为一组邻边求得点G的坐标即可.
解:(1)设A(a,0),B(0,b),
将A的坐标代入y=kx-4k(k≠0),得0=ka-4k,
解得a=4,
∵矩形的面积为12,
∴ab=12,
解得b=3,
∴A(4,0),B(0,3);
(2)∵D为AC的中点,
∴点D的坐标为(2,![]() ),
),
∵OE=1,
∴点E的坐标为(0,-1),
设直线EF的解析式为y=kx+b,将点D和点E的坐标代入得 ,
,
解得 ,
,
∴直线EF的解析式为y=![]() x-1;
x-1;
(3)存在;
理由:∵点F在BC上,
∴点F的纵坐标为3,
将y=3代入y=![]() x-1得
x-1得![]() x-1=3,
x-1=3,
解得:x=![]() ,
,
∴点F的坐标为(![]() ,3);
,3);
①如图1所示:

∵四边形CDFG为平行四边形,
∴GM=MD,CM=MF,
∴点M的坐标为(![]() ,3),
,3),
设点G的坐标为(x,y),
∴![]() ,
,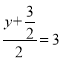 ,解得:x=
,解得:x=![]() ,y=
,y=![]() ,
,
∴点G的坐标为(![]() ,
,![]() );
);
②如图2所示:

∵点F的坐标为(![]() ,3),
,3),
∴CF=![]() ,
,
∵四边形CGDF为平行四边形,
∴CF∥GD,CF=GD,
∴点G的坐标为(![]() ,
,![]() );
);
③如图3所示:

∵四边形CGDF为平行四边形,
∴CF∥GD,CF=GD,
∴点G的坐标为(![]() ,
,![]() );
);
综上所述:点G的坐标为(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】4月23日是世界读书日,某校为了营造读书好、好读书、读好书的书香校园,决定采购《简·爱》、《小词大雅》两种图书供学生阅读,通过了解,购买2本《简·爱》和3本《小词大雅》共需168元,购买3本《简·爱》和2本《小词大雅》共需172元.
(1)求一本《简·爱》和《小词大雅》的价格分别是多少元;
(2)若该校计划购买两种图书共300本,其中《简·爱》的数量不多于《小词大雅》数量,且不少于100件.购买《简·爱》m本,求总费用W元与m之间的函数关系式,并写出m的取值范围;
(3)在(2)的条件下,学校在团购书籍时,商家店铺中《简·爱》正进行书籍促销活动,每本书箱降价a元(0< a <8),求学校购书的的最低总费用W1的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(0,a),B(0,b),C(m,b)且(a-4)2+
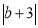 =0,
=0,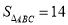
(1)求C点坐标
(2)作DE DC,交y轴于E点,EF为 AED的平分线,且DFE= 90o。 求证:FD平分ADO;
(3)E 在 y 轴负半轴上运动时,连 EC,点 P 为 AC 延长线上一点,EM 平分∠AEC,且 PM⊥EM,PN⊥x 轴于 N 点,PQ 平分∠APN,交 x 轴于 Q 点,则 E 在运动过程中,
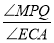 的大小是否发生变化,若不变,求出其值.
的大小是否发生变化,若不变,求出其值.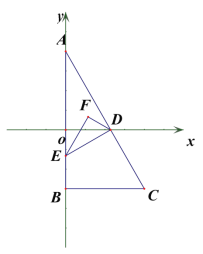
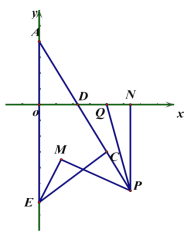
-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)停车难已成为合肥城市病之一,主要表现在居住停车位不足,停车资源结构性失衡,中心城区供需差距大等等.如图是张老师的车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,已知小汽车车门宽AO为 1.2 米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,AB//EF,∠2=2∠1

(1)证明∠FEC=∠FCE;
(2)如图2,M为AC上一点,N为FE延长线上一点,且∠FNM=∠FMN,则∠NMC与∠CFM有何数量关系,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.
(1)①在平行四边形,矩形,菱形、正方形中,一定是十字形的有 ;
②若凸四边形ABCD是十字形,AC=a,BD=b,则该四边形的面积为 ;
(2)如图1,以等腰Rt△ABC的底边AC为边作等边三角形△ACD,连接BD,交AC于点O, 当
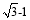 ≤S 四边形≤
≤S 四边形≤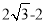 时,求BD的取值范围;
时,求BD的取值范围; (3)如图2,以十字形ABCD的对角线AC与BD为坐标轴,建立如图所示的平面直角坐标系xOy,若计 十字形ABCD的面积为S,记△AOB,△COD,△AOD,△BOC的面积分别为:S1,S2,S3,S4,且同时满足列四个条件:

①
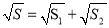 ;②
;② 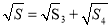 ;③十字形ABCD的周长为32:④∠ABC=60°; 若E为OA的中点,F为线段BO上一动点,连接EF,动点P从点E出发,以1cm/s 的速度沿线段EF匀速运动到点F,再以2cms 的速度沿线段FB匀速运动到点B,到达点B 后停止运动,当点P沿上述路线运动 到点B所需要的时间最短时,求点P走完全程所需的时间及直线EF的解析式.
;③十字形ABCD的周长为32:④∠ABC=60°; 若E为OA的中点,F为线段BO上一动点,连接EF,动点P从点E出发,以1cm/s 的速度沿线段EF匀速运动到点F,再以2cms 的速度沿线段FB匀速运动到点B,到达点B 后停止运动,当点P沿上述路线运动 到点B所需要的时间最短时,求点P走完全程所需的时间及直线EF的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:

(1)根据上表填空:
①抛物线与x轴的交点坐标是______和______;
②抛物线经过点(-3,______);
(2)试确定抛物线y=ax2+bx+c的解析式.
相关试题

