【题目】随着气温的升高,空调的需求量大增.某家电超市对每台进价分别为2000元、1700元的![]() 、
、![]() 两种型号的空调,近两周的销售情况统计如下:
两种型号的空调,近两周的销售情况统计如下:
销售时段 | 销售量 | 销售收入 | |
|
| ||
第一周 | 6台 | 7台 | 31000元 |
第二周 | 8台 | 11台 | 45000元 |
(1)求![]() 、
、![]() 两种型号的空调的销售价;
两种型号的空调的销售价;
(2)若该家电超市准备用不多于54000元的资金,采购这两种型号的空调30台,求![]() 种型号的空调最多能采购多少台?
种型号的空调最多能采购多少台?
(3)在(2)的条件下,该家电超市售完这30台空调能否实现利润不低于15800元的目标?若能,请给出采购方案.若不能,请说明理由.
参考答案:
【答案】(1)A、B两种型号空调的销售价分别为2600元和2200元;(2) 10台;(3)见解析.
【解析】
(1)设A、B两种型号电风扇的销售单价分别为x元、y元,根据6台A型号7台B型号的电扇收入31000元,8台A型号11台B型号的电扇收入45000元,列方程组求解即可;
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(30-a)台,根据金额不多余54000元,列不等式求解即可得出答案;
(3)设利润为15800元,列方程求出![]() ,分三种情况进行讨论,即可解答.
,分三种情况进行讨论,即可解答.
解:(1)设![]() 、
、![]() 两种型号的空调的销售价分别为
两种型号的空调的销售价分别为![]() 、
、![]() 元,
元,
则:![]() 解得:
解得:![]() ,
,
答:![]() 、
、![]() 两种型号空调的销售价分别为2600元和2200元.
两种型号空调的销售价分别为2600元和2200元.
(2)设采购![]() 种型号空调
种型号空调![]() 台,则采购
台,则采购![]() 种型号的空调
种型号的空调![]() 台
台
则![]() ,
,
解得:![]() ,答:最多采购
,答:最多采购![]() 种型号的空调10台.
种型号的空调10台.
(3)根据题意得:
![]() ,解得
,解得![]() ,
,
∵![]() ,∴
,∴![]()
∴共有3种方案:
方案①:![]() 型号空调8台,
型号空调8台,![]() 型号的空调22台;
型号的空调22台;
方案②:![]() 型号空调9台,
型号空调9台,![]() 型号的空调21台;
型号的空调21台;
方案③:![]() 型号空调10台,
型号空调10台,![]() 型号的空调20台.
型号的空调20台.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在矩形ABCD中,AD=
 AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,有下列结论:①∠AED=∠CED;②OE=OD;③△BEH≌△HDF;④BC﹣CF=2EH;⑤AB=FH.其中正确的结论有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,有下列结论:①∠AED=∠CED;②OE=OD;③△BEH≌△HDF;④BC﹣CF=2EH;⑤AB=FH.其中正确的结论有( )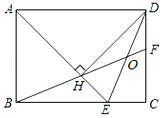
A. 5个 B. 4个 C. 3个 D. 2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
 ,点
,点 是直线
是直线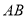 、
、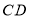 之间的一点,连接
之间的一点,连接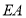 、
、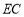 .
.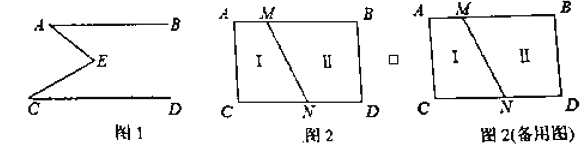
(1)问题发现:
①若
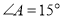 ,
, ,则
,则 ___________.
___________.②猜想图1中
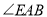 、
、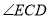 、
、 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.(2)拓展应用:
如图2,
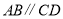 ,线段
,线段 把
把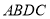 这个封闭区域分为Ⅰ、Ⅱ两部分(不含边界),点
这个封闭区域分为Ⅰ、Ⅱ两部分(不含边界),点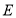 是位于这两个区域内的任意一点,请直接写出
是位于这两个区域内的任意一点,请直接写出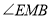 、
、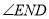 、
、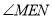 的数量关系.
的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛,成绩如图所示:
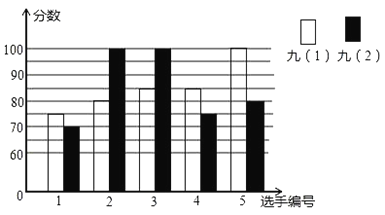
(1)根据图示填写下表;
班级
平均数(分)
中位数(分)
众数(分)
九(1)
85
九(2)
85
100
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)已知九(1)班复赛成绩的方差是70,请计算九(2)班的复赛成绩的方差,并说明哪个班的成绩比较稳定?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)已知:
 ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程 的两个实数根.
的两个实数根.(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么
 ABCD的周长是多少?
ABCD的周长是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解青少年形体情况,现随机抽查了某市若干名初中学生坐姿、站姿、走姿的好坏情况.我们对测评数据作了适当处理(如果一个学生有一种以上不良姿势,以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请你根据图中所给信息解答下列问题:
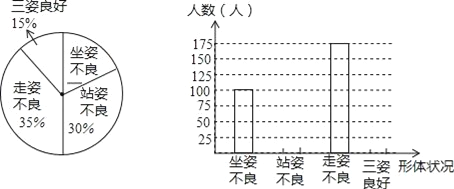
(1)请将两幅统计图补充完整;
(2)请问这次被抽查形体测评的学生一共是多少人?
(3)如果全市有5万名初中生,那么全市初中生中,坐姿和站姿不良的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】每逢金秋送爽之时,正是大闸蟹上市的旺季,也是吃蟹的最好时机,可谓膏肥黄美.


某经销商购进一批雌蟹、雄蟹共1000只,进价均为每只40元,然后以雌蟹每只75元、雄蟹每只60元的价格售完,共获利29000元.
(1)求该经销商分别购进雌蟹、雄蟹各多少只?
(2)民间有“九雌十雄”的说法,即九月吃雌蟹,十月吃雄蟹.十月份,在进价不变的情况下该经销商决定调整价格,将雌蟹的价格在九月份的基础上下调
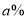 (降价后售价不低于进价),雄蟹的价格上涨
(降价后售价不低于进价),雄蟹的价格上涨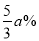 ,同时雌蟹的销量较九月下降了
,同时雌蟹的销量较九月下降了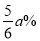 ,雄蟹的销量上升了
,雄蟹的销量上升了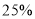 ,结果十月份的销售额比九月份增加了1000元,求a的值.
,结果十月份的销售额比九月份增加了1000元,求a的值.
相关试题

