【题目】(9分)已知:![]() ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么![]() ABCD的周长是多少?
ABCD的周长是多少?
参考答案:
【答案】解:(1)∵四边形ABCD是菱形,∴AB=AD。
又∵![]() ,
,
当![]() ,即m=1时,四边形ABCD是菱形。
,即m=1时,四边形ABCD是菱形。
把m=1代入![]() ,得
,得![]() 。
。
∴![]() 。
。
∴菱形ABCD的边长是![]() 。
。
(2)把AB=2代入![]() ,得
,得![]() ,解得
,解得![]() 。
。
把![]() 代入
代入![]() ,得
,得![]() 。
。
解得![]() ,
,![]() 。∴AD=
。∴AD=![]() 。
。
∵四边形ABCD是平行四边形,
∴□ABCD的周长是2(2+![]() )=5。
)=5。
【解析】
(1)根据菱形的性质可得出AB=AD,由根的判别式即可得出关于m的一元二次方程,解之即可得出m的值;
(2)将x=2代入一元二次方程可求出m的值,再根据根与系数的关系即可得出AB+AD的值,利用平行四边形的性质即可求出平行四边形ABCD的周长.
解:(1)∵四边形ABCD是菱形,
∴AB=AD,
∵AB、AD的长是关于x的一元二次方程x2﹣mx+![]() =0的两个实数根,
=0的两个实数根,
∴△=(﹣m)2﹣4(![]() )=m2﹣2m+1=0,
)=m2﹣2m+1=0,
解得:m=1.
∴当m为1时,四边形ABCD是菱形.
(2)将x=2代入x2﹣mx+![]() =0中,得:4﹣2m+
=0中,得:4﹣2m+![]() =0,
=0,
解得:m=![]() ,/p>
,/p>
∵AB、AD的长是关于x的一元二次方程x2﹣mx+![]() =0的两个实数根,
=0的两个实数根,
∴AB+AD=m=![]() ,
,
∴平行四边形ABCD的周长=2(AB+AD)=2×![]() =5.
=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知平行四边形
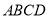 ,延长
,延长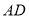 到
到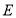 ,使
,使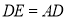 ,连接
,连接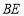 与
与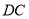 交于
交于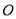 点.
点.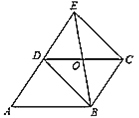
(1)求证:
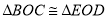 ;
; (2)当
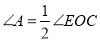 时,连续
时,连续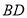 ,
,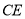 ,求证:四边形
,求证:四边形 为矩形.
为矩形. -
科目: 来源: 题型:
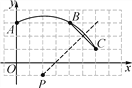
查看答案和解析>>【题目】如图,在平面直角坐标系中,一段圆弧经过格点A、B、C.(网格小正方形边长为1)
(1)请写出该圆弧所在圆的圆心P的坐标,并求⊙P的半径(结果保留根号);
(2)判断点M(-1,1)与⊙P的位置关系.
-
科目: 来源: 题型:
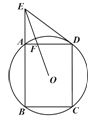
查看答案和解析>>【题目】如图,矩形ABCD接于半径为2.5的⊙O,AB=4, 延长BA到E,使AE=
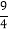 ,连接ED.
,连接ED.(1)求证:直线ED是⊙O的切线;
(2)连接EO交AD于F,求FO的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)
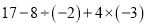
(2)
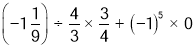
(3)﹣32×4﹣(﹣5)×7﹣(﹣2)3
(4)(﹣1)2018+|﹣5|×(﹣
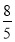 )﹣(﹣4)2÷(﹣8)
)﹣(﹣4)2÷(﹣8) -
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图①,若点E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有一座弧形的拱桥,桥下水面的宽度AB为7.2米,拱顶高出水面CD的长为2.4米,现有一艘宽3米,船舱顶部为长方形并且高出水面2米的货船要经过这里,此货船能顺利通过这座弧形拱桥吗?

相关试题

