【题目】每逢金秋送爽之时,正是大闸蟹上市的旺季,也是吃蟹的最好时机,可谓膏肥黄美.


某经销商购进一批雌蟹、雄蟹共1000只,进价均为每只40元,然后以雌蟹每只75元、雄蟹每只60元的价格售完,共获利29000元.
(1)求该经销商分别购进雌蟹、雄蟹各多少只?
(2)民间有“九雌十雄”的说法,即九月吃雌蟹,十月吃雄蟹.十月份,在进价不变的情况下该经销商决定调整价格,将雌蟹的价格在九月份的基础上下调![]() (降价后售价不低于进价),雄蟹的价格上涨
(降价后售价不低于进价),雄蟹的价格上涨![]() ,同时雌蟹的销量较九月下降了
,同时雌蟹的销量较九月下降了![]() ,雄蟹的销量上升了
,雄蟹的销量上升了![]() ,结果十月份的销售额比九月份增加了1000元,求a的值.
,结果十月份的销售额比九月份增加了1000元,求a的值.
参考答案:
【答案】(1)雌蟹购进600只,则雄蟹购进400只;(2)a=20.
【解析】试题分析:(1)直接根据题意表示出雌蟹与雄蟹总利润进而得出等式,求出答案;
(2)利用价格与销量的变化表示出销售额,进而得出等式求出答案.
试题解析:解:(1)设雌蟹购进x只,则雄蟹购进(1000﹣x)只,根据题意可得:
(75﹣40)x+(60﹣40)(1000﹣x)=29000
解得:x=600,则1000﹣600=400(只).
答:雌蟹600只,雄蟹400只;
(2)十月份的销售额=75×600+60×400+1000=70000,则:
75(1﹣a%)×600(1﹣![]() a%)+60(1+
a%)+60(1+![]() a%)×400(1+25%)=70000
a%)×400(1+25%)=70000
令a%=t,整理得:15t2﹣13t+2=0,解得:t1=![]() ,t2=
,t2=![]() .
.
当t=![]() 时,售价=75×(1﹣
时,售价=75×(1﹣![]() )=25<40,不合题意舍去;
)=25<40,不合题意舍去;
当t=![]() 时,售价=75×(1﹣
时,售价=75×(1﹣![]() )=60>40,故a=20.
)=60>40,故a=20.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着气温的升高,空调的需求量大增.某家电超市对每台进价分别为2000元、1700元的
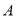 、
、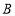 两种型号的空调,近两周的销售情况统计如下:
两种型号的空调,近两周的销售情况统计如下:销售时段
销售量
销售收入
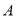 型号
型号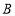 型号
型号第一周
6台
7台
31000元
第二周
8台
11台
45000元
(1)求
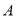 、
、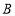 两种型号的空调的销售价;
两种型号的空调的销售价;(2)若该家电超市准备用不多于54000元的资金,采购这两种型号的空调30台,求
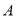 种型号的空调最多能采购多少台?
种型号的空调最多能采购多少台?(3)在(2)的条件下,该家电超市售完这30台空调能否实现利润不低于15800元的目标?若能,请给出采购方案.若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)已知:
 ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程 的两个实数根.
的两个实数根.(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么
 ABCD的周长是多少?
ABCD的周长是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解青少年形体情况,现随机抽查了某市若干名初中学生坐姿、站姿、走姿的好坏情况.我们对测评数据作了适当处理(如果一个学生有一种以上不良姿势,以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请你根据图中所给信息解答下列问题:
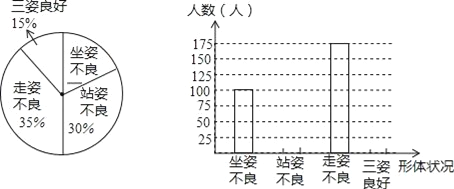
(1)请将两幅统计图补充完整;
(2)请问这次被抽查形体测评的学生一共是多少人?
(3)如果全市有5万名初中生,那么全市初中生中,坐姿和站姿不良的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】由几个相同的边长为1的小立方块搭成的几何体的俯视图如图①,格中的数字表示该位置的小立方块的个数.
(1)请在下面方格纸图②中分别画出这个几何体的主视图和左视图.
(2)根据三视图,这个组合几何体的表面积为多少个平方单位?(包括底面积)
(3)若上述小立方块搭成的几何体的俯视图不变,如图③,各位置的小立方块个数可以改变(总数目不变),则搭成这样的组合几何体中的表面积最大(包括底面积)仿照图①,将数字填写在图③的正方形中.
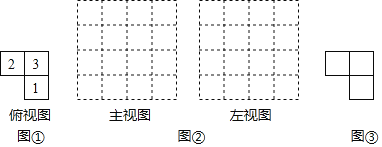
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(p,0),B(0,q),且p、q满足(p﹣2)2+
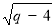 =0.
=0.(1)求直线AB的解析式;
(2)若点M为直线y=mx上一点,且△ABM是以AB为底的等腰直角三角形,求m值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的证明过程,指出其错误.(在错误部分下方划线)已知△ABC,求证:∠A+∠B+∠C=180°
(1)证明:过A作DE∥BC,且使∠1=∠C
∵DE∥BC(作图)
∴∠2=∠B(内错角相等两直线平行)
∵∠1=∠C(作图)
∴∠B+∠C+∠3=∠2+∠1+∠3(等量代换)
∠2+∠l+∠3=180°(周角的定义)
即∠BAC+∠B+∠C=180°(等量代换)
(2)类比探究:请同学们参考图2,模仿(1)的解决过程,避免(1)中的错误,试说明求证:∠A+∠B+∠C=180°
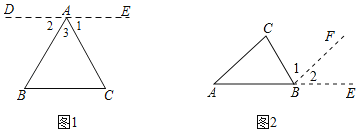
相关试题

