搜索
【题目】如图，菱形
中，
，
.点
、
分别为
、
的中点，连接
、
、EF，则
的周长为
A. 9B. 
C. 
D. 
参考答案：
【答案】B
【解析】
首先根据菱形的性质证明△ABE≌△ADF，然后连接AC可推出△ABC以及△ACD为等边三角形．根据等腰三角形三线合一的定理又可推出△AEF是等边三角形．根据勾股定理可求出AE的长，即可求出周长．
解：连接AC，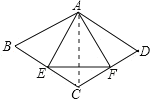
∵四边形ABCD是菱形，
∴AB=AD=BC=CD，∠B=∠D，∠B=180°-∠BCD=60°
∵E、F分别是BC、CD的中点，
∴BE=DF，
在△ABE和△ADF中，
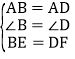
∴△ABE≌△ADF（SAS），
∴AE=AF，∠BAE=∠DAF．
∵∠B=∠D=60°，
∴△ABC与△ACD是等边三角形，
∴AE⊥BC，AF⊥CD，
∴∠BAE=∠DAF=30°，
∴∠EAF=60°，
∴△AEF是等边三角形．
∵ AB=2，
∴AE=
，
∴△AEF的周长是3 ．
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图一条抛物线
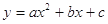（a≠0）与x轴有两个交点，那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”．
（1）“抛物线三角形”一定是_______________三角形；
（2）若抛物线y=－x2+bx（b＞0）的“抛物线三角形”是等腰直角三角形，求b的值；
（3）如图，△OAB是抛物线y=－x2+b′x（b′＞0）的“抛物线三角形”，是否存在以原点O为对称中心的矩形ABCD？若存在，求出过O、C、D三点的抛物线的表达式；若不存在，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】列一元一次方程解应用题：
学生在素质教育基地进行社会实践活动，帮助农民伯伯采摘了黄瓜和茄子共80千克，了解到这些蔬菜的种植成本共180元，还了解到如下信息：
（1）求采摘的黄瓜和茄子各多少千克？
（2）这些采摘的黄瓜和茄子可赚多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知直线y=x+3与x轴交于点A，与y轴交于点B，将直线在x轴下方的部分沿x轴翻折，得到一个新函数的图象（图中的“V形折线”）．
（1）类比研究函数图象的方法，请列举新函数的两条性质，并求新函数的解析式；
（2）如图2，双曲线y=
与新函数的图象交于点C（1，a），点D是线段AC上一动点（不包括端点），过点D作x轴的平行线，与新函数图象交于另一点E，与双曲线交于点P．①试求△PAD的面积的最大值；
②探索：在点D运动的过程中，四边形PAEC能否为平行四边形？若能，求出此时点D的坐标；若不能，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】(1)如图甲，点O在直线AB上，OC 平分∠AOD，∠BOD= 42°12′，求∠AOC的度数.
(2)已知，如图乙，B、C 两点把线段AD 分成2：5：3三部分，M为AD的中点，BM=6cm，求CM和AD的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算或化简:
(1)计算:(-2)×
÷(-
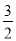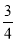)×4+(- 2)3;(2)计算:(-1)2019-(1-
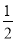)÷3×[3-(-3)2];(3)化简:4a2- 2(a2- b2)- 3(a2+ b2).
-
科目： 来源： 题型：
查看答案和解析>>【题目】按要求解下列各题:
(1)先化简，再求值:5(a2b + 2ab2)- 2(3a2b + 4ab2-1),其中|a-2|+(b+ 3)2= 0:
(2)解方程:
=1-
.
相关试题
