【题目】(1)如图甲,点O在直线AB上,OC 平分∠AOD,∠BOD= 42°12′,求∠AOC的度数.
(2)已知,如图乙,B、C 两点把线段AD 分成2:5:3三部分,M为AD的中点,BM=6cm,求CM和AD的长.

参考答案:
【答案】(1)68°54′;(2)4,20
【解析】
(1)根据题意找出这几个角之间的关系,利用角平分线的性质来求.
(2)由已知B,C两点把线段AD分成2:5:3三部分,所以设AB=2xcm,BC=5xcm,CD=3xcm,根据已知分别用x表示出AD,MD,从而得出BM,继而求出x,则求出CM和AD的长.
解:(1)∵∠AOB=180°,
∴∠AOD=180°-∠BOD=180°-42°12′=137°48′,
∵OC平分∠AOD,
∴∠AOC=![]() ∠AOD=
∠AOD=![]() ×137°48′=68°54′.
×137°48′=68°54′.
(2)设AB=2xcm,BC=5xcm,CD=3xcm
∴AD=AB+BC+CD=10xcm
∵M是AD的中点
∴AM=MD=![]() AD=5xcm
AD=5xcm
∴BM=AM-AB=5x-2x=3xcm
∵BM=6cm,
∴3x=6,x=2
故CM=MD-CD=5x-3x=2x=2×2=4cm,
AD=10x=10×2=20cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列一元一次方程解应用题:
学生在素质教育基地进行社会实践活动,帮助农民伯伯采摘了黄瓜和茄子共80千克,了解到这些蔬菜的种植成本共180元,还了解到如下信息:
(1)求采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子可赚多少元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x轴下方的部分沿x轴翻折,得到一个新函数的图象(图中的“V形折线”).

(1)类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;
(2)如图2,双曲线y=
 与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.①试求△PAD的面积的最大值;
②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形
 中,
中, ,
, .点
.点 、
、 分别为
分别为 、
、 的中点,连接
的中点,连接 、
、 、EF,则
、EF,则 的周长为
的周长为
A. 9B.
 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算或化简:
(1)计算:(-2)×
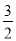 ÷(-
÷(-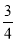 )×4+(- 2)3;
)×4+(- 2)3;(2)计算:(-1)2019-(1-
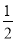 )÷3×[3-(-3)2];
)÷3×[3-(-3)2];(3)化简:4a2- 2(a2- b2)- 3(a2+ b2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】按要求解下列各题:
(1)先化简,再求值:5(a2b + 2ab2)- 2(3a2b + 4ab2-1),其中|a-2|+(b+ 3)2= 0:
(2)解方程:
 =1-
=1- .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读:设试验结果落在某个区域S中每一点的机会均等,用A表示事件“试验结果落在S中的一个小区域M中”,那么事件A发生的概率P(A)
 .在桌面上放一张50 cm×50 cm的正方形白纸ABCD,⊙O是它的内切圆,小明随机地将1000粒大米撒到该白纸上,其中落在圆内的大米有800粒,由此可得圆周率
.在桌面上放一张50 cm×50 cm的正方形白纸ABCD,⊙O是它的内切圆,小明随机地将1000粒大米撒到该白纸上,其中落在圆内的大米有800粒,由此可得圆周率 的值为( )
的值为( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

