【题目】如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,将直线在x轴下方的部分沿x轴翻折,得到一个新函数的图象(图中的“V形折线”).

(1)类比研究函数图象的方法,请列举新函数的两条性质,并求新函数的解析式;
(2)如图2,双曲线y=![]() 与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
①试求△PAD的面积的最大值;
②探索:在点D运动的过程中,四边形PAEC能否为平行四边形?若能,求出此时点D的坐标;若不能,请说明理由.
参考答案:
【答案】(1)y=![]() ;(2)①
;(2)①![]() ;②在点D运动的过程中,四边形PAEC不能为平行四边形.理由见解析.
;②在点D运动的过程中,四边形PAEC不能为平行四边形.理由见解析.
【解析】(1)根据一次函数的性质,结合函数图象可写出新函数的两条性质;求新函数的解析式,可分两种情况进行讨论:①x≥-3时,显然y=x+3;②当x<-3时,利用待定系数法求解;
(2)①先把点C(1,a)代入y=x+3,求出C(1,4),再利用待定系数法求出反比例函数解析式为y=![]() .由点D是线段AC上一动点(不包括端点),可设点D的坐标为(m,m+3),且-3<m<1,那么P(
.由点D是线段AC上一动点(不包括端点),可设点D的坐标为(m,m+3),且-3<m<1,那么P(![]() ,m+3),PD=
,m+3),PD=![]() -m,再根据三角形的面积公式得出△PAD的面积为S=
-m,再根据三角形的面积公式得出△PAD的面积为S=![]() (
(![]() -m)×(m+3)=-
-m)×(m+3)=-![]() m2-
m2-![]() m+2=-
m+2=-![]() (m+
(m+![]() )2+
)2+![]() ,然后利用二次函数的性质即可求解;
,然后利用二次函数的性质即可求解;
②先利用中点坐标公式求出AC的中点D的坐标,再计算DP,DE的长度,如果DP=DE,那么根据对角线互相平分的四边形是平行四边形可得四边形PAEC为平行四边形;如果DP≠DE,那么不是平行四边形.
试题解析:(1)如图1,均是正整数新函数的两条性质:①函数的最小值为0;

②函数图象的对称轴为直线x=-3;
由题意得A点坐标为(-3,0).分两种情况:
①x≥-3时,显然y=x+3;
②当x<-3时,设其解析式为y=kx+b.
在直线y=x+3中,当x=-4时,y=-1,
则点(-4,-1)关于x轴的对称点为(-4,1).
把(-4,1),(-3,0)代入y=kx+b,
得![]()
解得![]()
∴y=-x-3.
综上所述,新函数的解析式为y= ;
;
(2)如图2,

①∵点C(1,a)在直线y=x+3上,
∴a=1+3=4.
∵点C(1,4)在双曲线y=![]() 上,
上,
∴k=1×4=4,y=![]() .
.
∵点D是线段AC上一动点(不包括端点),
∴可设点D的坐标为(m,m+3),且-3<m<1.
∵DP∥x轴,且点P在双曲线上,
∴P(![]() ,m+3),
,m+3),
∴PD=![]() -m,
-m,
∴△PAD的面积为
S=![]() (
(![]() -m)×(m+3)=-
-m)×(m+3)=-![]() m2-
m2-![]() m+2=-
m+2=-![]() (m+
(m+![]() )2+
)2+![]() ,
,
∵a=-![]() <0,
<0,
∴当m=-![]() 时,S有最大值,为
时,S有最大值,为![]() ,
,
又∵-3<-![]() <1,
<1,
∴△PAD的面积的最大值为![]() ;
;
②在点D运动的过程中,四边形PAEC不能为平行四边形.理由如下:
当点D为AC的中点时,其坐标为(-1,2),此时P点的坐标为(2,2),E点的坐标为(-5,2),
∵DP=3,DE=4,
∴EP与AC不能互相平分,
∴四边形PAEC不能为平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有8筐白菜,以每筐25千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的纪录如下:

回答下列问题:
(1)这8筐白菜中最接近标准重量的这筐白菜重__________千克;
(2)与标准重量比较,8筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.6元,则出售这8筐白菜可卖多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】青岛交运集团出租车司机张师傅某天下午的营运全是在东西走向的吉林路上进行的,如果规定向东为正,向西为负,他这天下午行车里程
 单位:千米
单位:千米 如下:
如下: ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,
(1)张师傅这天最后到达目的地时,在下午出车时的出发地哪个方向?距离出发地多远?
(2)张师傅这天下午共行车多少千米?
(3)若每千米耗油
 ,则这天下午张师傅用了多少升油?
,则这天下午张师傅用了多少升油? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是反比例函数y=
 (m<0)位于第二象限的图像上的一个动点,过点A作AC⊥x
(m<0)位于第二象限的图像上的一个动点,过点A作AC⊥x轴于点C;M为是线段AC的中点,过点M作AC的垂线,与反比例函数的图像及y轴分别交于B、
D两点.顺次连接A、B、C、D.设点A的横坐标为n.
(1)求点B的坐标(用含有m、n的代数式表示);
(2)求证:四边形ABCD是菱形;
(3)若△ABM的面积为2,当四边形ABCD是正方形时,求直线AB的函数表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,sinA=
 ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.(1)求线段CD的长;
(2)求cos∠ABE的值。

-
科目: 来源: 题型:
查看答案和解析>>【题目】按图示方法用小棒摆正六边形,摆15个正六边形需要(__________)根小棒;摆n个正六边形需要(__________)根小棒.


-
科目: 来源: 题型:
查看答案和解析>>【题目】直接写得数.
1÷0.005= 7.8+3.02= 0.5×0.02= 75%-0.69= 0.023=
 +0.025=
+0.025=  ÷0.0625=
÷0.0625=  = 1.2-
= 1.2-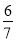 ×0= 102×41≈
×0= 102×41≈
相关试题

