【题目】列一元一次方程解应用题:
学生在素质教育基地进行社会实践活动,帮助农民伯伯采摘了黄瓜和茄子共80千克,了解到这些蔬菜的种植成本共180元,还了解到如下信息:
(1)求采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子可赚多少元?

参考答案:
【答案】(1)采摘的黄瓜30千克,茄子50千克;(2)可赚110元.
【解析】
(1)设采摘的黄瓜x千克,则茄子(80﹣x)千克,根据题意可得等量关系:黄瓜的成本+茄子的成本=180元,根据等量关系列出方程,再解即可;
(2)根据(1)中的结果计算出黄瓜的利润和茄子的利润,再求和即可.
(1)设采摘的黄瓜x千克,则茄子(80﹣x)千克,由题意得:
2x+2.4(80﹣x)=180
解得:x=30.
当x=30时,80﹣30=50(千克).
答:采摘的黄瓜30千克,则茄子50千克;
(2)(3﹣2)×30+(4﹣2.4)×50=30+80=110(元).
答:采摘的黄瓜和茄子可赚110元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)某商场用2500元购进了A、B两种新型节能台灯共50盏,这两种台灯的进价,标价如下表所示:

(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的九折出售,B型台灯按标价的八折出售,那么这批台灯全部售完后,商场共获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在半径为50的⊙O中,弦AB的长为50,
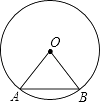
(1)求∠AOB的度数;
(2)求点O到AB的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段MN=3cm,在线段MN上取一点P,使PM=PN;延长线段MN到点A,使AN=
 MN;延长线段NM到点B,使BN=3BM.
MN;延长线段NM到点B,使BN=3BM.(1)根据题意,画出图形;
(2)求线段AB的长;
(3)试说明点P是哪些线段的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请根据下面X与Y的对话解答下列各小题:
X:我和Y都是多边形,我们俩的内角和相加的结果为1440°;
Y:X的边数与我的边数之比为1∶3.
(1)求X与Y的外角和相加的度数;
(2)分别求出X与Y的边数;
(3)试求出Y共有多少条对角线?
相关试题

