【题目】如图一条抛物线
（a≠0）与x轴有两个交点，那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”．
（1）“抛物线三角形”一定是_______________三角形；
（2）若抛物线y=－x2+bx（b＞0）的“抛物线三角形”是等腰直角三角形，求b的值；
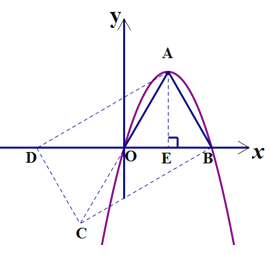
（3）如图，△OAB是抛物线y=－x2+b′x（b′＞0）的“抛物线三角形”，是否存在以原点O为对称中心的矩形ABCD？若存在，求出过O、C、D三点的抛物线的表达式；若不存在，说明理由．
【答案】（1）等腰；（2）b=2；（3）y=x+2
x．
【解析】试题分析：(1)、根据抛物线的性质可得三角形为等腰三角形；(2)、首先根据y=0求出点B的坐标，然后根据等腰三角形的性质求出b的值；(3)、首先作△OCD和△OAB成中心对称图形，根据矩形的性质求出OE和OA的长度，然后根据三角形的性质求出b′的值，根据b′的值求出点C、D的坐标，最后利用待定系数法求出函数解析式.
试题解析：(1)、等腰
(2)、当y=0时，－x+bx=0 解得：
=0，
=b ∴B（b,0），即：OB=b
∵抛物线y=－x+bx的顶点A的坐标为（
，
）， 且“抛物线三角形”是等腰直角三角形
∴=解得：
=0（舍去），
=2 ∴b的值为2
(3)、存在， 如图，作△OCD与△OAB关于原点O成中心对称，
则四边形ABCD是平行四边形，当OA=OB时，四边形ABCD为矩形
∵OA=OB，OA=AB ∴△OAB是等边三角形 过点A作AE⊥OB于E，则∠OAE=30°，OE=
∴OA=
∵顶点A（，
）， ∴=
解得：
=0（舍去），
=2
∴A（，3），B（2，0)
∴C（－，－3），D（－2，0）
设过C、D、O的解析式为y=ax+mx（a≠0），则
解得：
∴所求抛物线的解析式为y=x+2x.
科目：初中数学 来源： 题型：
【题目】四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM．
(1)求证：AM=AD+MC．
(2)若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，试判断AM=AD+MC是否成立？若成立，请给出证明，若不成立，请说明理由；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知等边△ABC中，D为边AC上一点．
（1）以BD为边作等边△BDE，连接CE，求证：AD=CE；
（2）如果以BD为斜边作Rt△BDE，且∠BDE=30°，连接CE并延长，与AB的延长线交于F点，求证：AD=BF；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】西安市某中学九年级组织了一次数学计算比赛（禁用计算器），每班选25名同学参加比赛，成绩分为A，B，C，D四个等级，其中A等级得分为100分，B等级得分为85分，C等级得分为75分，D等级得分为60分，数学教研组将九年级一班和二班的成绩整理并绘制成如下的统计图，请根据提供的信息解答下列问题．
（1）把一班竞赛成绩统计图补充完整．
（2）填表：
平均数（分） | 中位数（分） | 众数（分） | |
一班 |
|
| 85 |
二班 | 84 | 75 |
|
（3）请从以下给出的两个方面对这次比赛成绩的结果进行①从平均数、众数方面来比较一班和二班的成绩；②从B级以上（包括B级）的人数方面来比较一班和二班的成绩．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是明代数学家程大位的《算法统宗》中的一个问题,其大意为:有一群人分银子，如果每人分七两，则剩余四两;如果每人分九两，则还差八两(注:明代时1斤= 16两，故有“半斤八两”这个成语.则下列设未知数列方程正确的序号是____.
①设这群人人数为x,根据题意得7x- 4=9x+ 8;
②设这群人人数为x,根据题意得7x+ 4= 9x一8;
③设所分银子的数量为x两，根据题意得
=
④设所分银子的数量为x两，根据题意得
=
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算或化简:
(1)计算:(-2)×
÷(-
)×4+(- 2)3;
(2)计算:(-1)2019-(1-
)÷3×[3-(-3)2];
(3)化简:4a2- 2(a2- b2)- 3(a2+ b2).
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点A,O,E在同一条直线上,∠BOD= 90°,OD是∠COE的角平分线，找出图中与∠DOE互余的角.甲、乙、丙三个同学的答案如下:
甲:只有一个角，是∠AOB:
乙:有两个角，是∠AOB和∠BOC:
丙:有三个角，是∠AOB,∠BOC,∠COD.
(1)请你判断哪个同学的答案是正确的?
(2)请你说明正确答案的理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】泰兴出租车司机小李某天下午的营运全是在东西走向的国庆路上进行的，若规定向东为正，向西为负，这天下午的行车里程如下（单位：千米）：
，
，
，
，
，
，
（单位：千米）.
（1）将最后一名乘客送到目的地后，小李距下午出发地点的距离是多少千米？
（2）若出租车每行驶
耗油
，这天下午这辆出租车共消耗多少升汽油？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一列快车从甲地匀速驶往乙地，一列慢车从乙地匀速驶往甲地，设先发出车辆行驶的时间为 xh , 两车之间的距离为ykm,图中的折线表示 y与x之间的函数关系。根据图象回答下列问题：
（1）慢车的速度为________ km/h,快车的速度为__________km/h;
（2）求线段CD所表示的y与x之间的函数关系式，并写出自变量 x的取值范围；
（3）当 x取何值时，两车之间的距离为300 km?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com