【题目】用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2+2ab+a.如:1☆3=1×32+2×1×3+1=16.
(1)求(﹣2)☆3的值;
(2)若( ![]() ☆3)☆(-
☆3)☆(- ![]() )=8,求a的值;
)=8,求a的值;
(3)若2☆x=m,( ![]() x)☆3=n(其中x为有理数),试比较m,n的大小.
x)☆3=n(其中x为有理数),试比较m,n的大小.
参考答案:
【答案】
(1)解:(﹣2)☆3=﹣2×32+2×(﹣2)×3+(﹣2)=﹣18﹣12﹣2 =﹣32;
(2)解: ![]() ☆3=
☆3= ![]() ×32+2×
×32+2× ![]() ×3+
×3+ ![]() =8(a+1) 解得:a=3;
=8(a+1) 解得:a=3;
(3)解:由题意m=2x2+2×2x+2=2x2+4x+2,
n= ![]() ×32+2×
×32+2× ![]() x×3+
x×3+ ![]() =4x, 所以m﹣n=2x2+2>0. 所以m>n.
=4x, 所以m﹣n=2x2+2>0. 所以m>n.
【解析】(1)根据题中规定a☆b=ab2+2ab+a,代入求解即可;
(2)根据题中定义的新运算“☆”,转化为关于a的一元一次方程,解方程即可;
(3)根据题中定义的新运算“☆”,分别表示出m与n的代数式,利用作差法求得m﹣n>0. 所以m>n.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各对数中,相等的一对数是( )
A.(﹣2)3与﹣23
B.﹣22与(﹣2)2
C.﹣(﹣3)与﹣|﹣3|
D.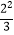 与(
与(  )2
)2 -
科目: 来源: 题型:
查看答案和解析>>【题目】若抛物线L:
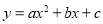 (a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系.此时,直线l叫做抛物线L的“带线”,抛物线L叫做直线l的“路线”.
(a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系.此时,直线l叫做抛物线L的“带线”,抛物线L叫做直线l的“路线”.(1)若直线y=mx+1与抛物线
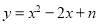 具有“一带一路”关系,求m,n的值;
具有“一带一路”关系,求m,n的值;(2)若某“路线”L的顶点在反比例函数
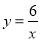 的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;
的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;(3)当常数k满足
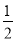 ≤k≤2时,求抛物线L:
≤k≤2时,求抛物线L: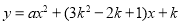 的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
的“带线”l与x轴,y轴所围成的三角形面积的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系内,点M(a+3,a-2)在y轴上,则点M的坐标是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】科技馆是少年儿童节假日游玩的乐园.
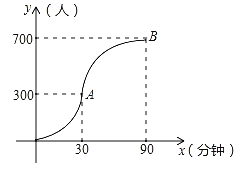
如图所示,图中点的横坐标x表示科技馆从8:30开门后经过的时间(分钟),纵坐标y表示到达科技馆的总人数.图中曲线对应的函数解析式为
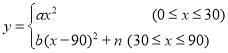 ,10:00之后来的游客较少可忽略不计.
,10:00之后来的游客较少可忽略不计.(1)请写出图中曲线对应的函数解析式;
(2)为保证科技馆内游客的游玩质量,馆内人数不超过684人,后来的人在馆外休息区等待.从10:30开始到12:00馆内陆续有人离馆,平均每分钟离馆4人,直到馆内人数减少到624人时,馆外等待的游客可全部进入.请问馆外游客最多等待多少分钟?
-
科目: 来源: 题型:
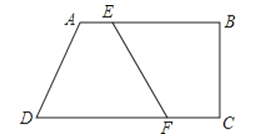
查看答案和解析>>【题目】如图,四边形ABCD中,AB∥CD,AB⊥BC,点E在AB边上从A向B以1cm/s的速度移动,同时点F在CD边上从C向D以2cm/s的速度移动,若AB=7cm,CD=9cm,则 秒时四边形ADFE是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c图象上部分点的坐标满足下表:
x
…
-3
-2
-1
0
1
…
y
…
-3
-2
-3
-6
-11
…
则该函数图象上的点(﹣6,y1),(m2+2m+3,y2)则下列选项正确的是( )
A.y1>y2B.y1≥y2C.y1<y2D.y1≤y2
相关试题

