【题目】如图,直线L:![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,在y轴上有一点
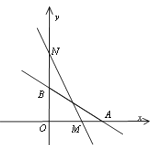
两点,在y轴上有一点![]() ,动点M从A点出发以每秒1个单位的速度沿射线AO匀速运动.
,动点M从A点出发以每秒1个单位的速度沿射线AO匀速运动.
(1)点A的坐标: ;点B的坐标: ;
(2)求△NOM的面积S与M的移动时间t之间的函数关系式;
(3)当![]() 为何值时,
为何值时,![]() ,求出此时点M的坐标;
,求出此时点M的坐标;
参考答案:
【答案】(1)(8,0),(0,6);(2)①当点M在y轴右侧时,OM=OA-AM=8-t,![]() (0≤t<8);②当点M在y轴左侧时,OM=AM-OA=t-8;
(0≤t<8);②当点M在y轴左侧时,OM=AM-OA=t-8;![]() (t>8);(3)当t=5或11时,
(t>8);(3)当t=5或11时,![]() ,此时点M的坐标分别为(3,0),(-3,0).
,此时点M的坐标分别为(3,0),(-3,0).
【解析】
(1)在![]() 中,分别令y=0和x=0,则可求得A、B的坐标;
中,分别令y=0和x=0,则可求得A、B的坐标;
(2)利用t可表示出OM,则可表示出S,注意分M在y轴右侧和左侧两种情况;
(3)由![]() ,建立关于时间t一元一次方程算出t值,即可得到M点坐标.
,建立关于时间t一元一次方程算出t值,即可得到M点坐标.
解:(1)依题意,令x=0,则有y=6,令y=0,则有x=8,故点A的坐标为(8,0),点B的坐标为(0,6);
(2)依题意,AM=t,
①当点M在y轴右侧时,OM=OA-AM=8-t;![]() (0≤t<8)
(0≤t<8)
②当点M在y轴左侧时,OM=AM-OA=t-8. ![]() (t>8)
(t>8)
(3)∵ON=8,![]() ;
;
![]() ,
,
①当点M在y轴右侧时,![]() ,解得t=5;此时M的坐标为(3,0).
,解得t=5;此时M的坐标为(3,0).
②当点M在y轴左侧时,![]() ,解得t=11,此时M的坐标为(-3,0)
,解得t=11,此时M的坐标为(-3,0)
综上:当t=5或11时,![]() ,此时点M的坐标分别为(3,0),(-3,0).
,此时点M的坐标分别为(3,0),(-3,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点O为直线AB上一点,∠COD=90°,射线OE平分∠AOD.
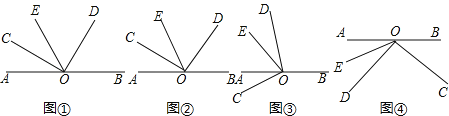
(1)如图①所示,若∠COE=20°,则∠BOD= °.
(2)若将∠COD绕点O旋转至图②的位置,试判断∠BOD和∠COE的数量关系,并说明理由;
(3)若将∠COD绕点O旋转至图③的位置,∠BOD和∠COE的数量关系是否发生变化?并请说明理由.
(4)若将∠COD绕点O旋转至图④的位置,继续探究∠BOD和∠COE的数量关系,请直接写出∠BOD和∠COE之间的数量关系: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,△ABC与△DEF都是等腰直角三角形,∠ACB=∠EDF=90°,且点D在AB边上,AB、EF的中点均为O,连结BF、CD、CO,显然点C、F、O在同一条直线上,可以证明△BOF≌△COD,则BF=CD.
解决问题
(1)将图①中的Rt△DEF绕点O旋转得到图②,猜想此时线段BF与CD的数量关系,并证明你的结论;
(2)如图③,若△ABC与△DEF都是等边三角形,AB、EF的中点均为O,上述(1)中的结论仍然成立吗?如果成立,请说明理由;如不成立,请求出BF与CD之间的数量关系;
(3)如图④,若△ABC与△DEF都是等腰三角形,AB、EF的中点均为0,且顶角∠ACB=∠EDF=α,请直接写出
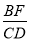 的值(用含α的式子表示出来)
的值(用含α的式子表示出来)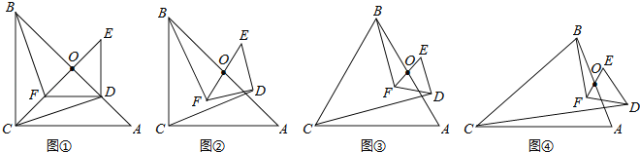
-
科目: 来源: 题型:
查看答案和解析>>【题目】我县近两个多月持续高温而且没有降雨导致居民用水严重紧缺,为了加强市民的节水意识,我县制定了如下用水收费标准:每户每月的用水不超过10吨时,水价为每吨2元,超过10吨时,超过的部分按每吨3元收费.该市某户居民5月份用水x吨,应交水费y元.
(1)若0<x≤10,请写出y与x的函数关系式.
(2)若x>10,请写出y与x的函数关系式.
(3)如果该户居民这个月交水费29元,那么这个月该户用水多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次根式的化简中,若被开方数还有根号,有的能将被开方数化成另一个二次根式的平方的形式,比如:
 ,聪明的你可以继续探究,当a,b,m,n为正整数时,若
,聪明的你可以继续探究,当a,b,m,n为正整数时,若 ,则有
,则有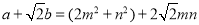 ,所以
,所以 .模仿上述探究解决下列问题:
.模仿上述探究解决下列问题:(1)当a,b,m,n为正整数时,
 ,请用含m,n的代数式分别表示a,b:a= ,b= .
,请用含m,n的代数式分别表示a,b:a= ,b= .(2)填空:
 =( +
=( +  )2
)2(3)若
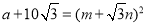 ,且a,m,n均为正整数,求a的值.
,且a,m,n均为正整数,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】有下列命题:①两条直线被第三条直线所截,同位角相等;②0.1的算术平方根是0.01;③算术平方根等于它本身的数是1;④如果点P(3-2n,1)到两坐标轴的距离相等,则n=1;⑤若a2=b2,则a=b;⑥若
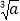 =
=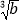 ,则a=b.其中假命题的个数是( )
,则a=b.其中假命题的个数是( )A. 3个B. 4个C. 5个D. 6个
-
科目: 来源: 题型:
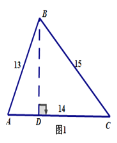
查看答案和解析>>【题目】(1)特例求解:在△ABC中,若三角形的三边为6、8、10,则这个三角形的面积 为 .
(2)一般化探究:在三角形ABC中,若AB=13,AC=14,BC=15,求△ABC的面积.
(3)模型建立:在图1三角形中,分别以AB,BC为边向外作正方形ABDE和正方形BCFG,试说明S△ABC=S△BDG.(温馨提示:作DP
 BG,AH
BG,AH BC)
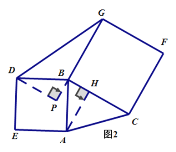
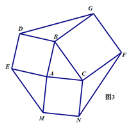
BC)(4)模型应用:分别以图1中三角形的三边为边向外作正方形ABDE、正方形BCFG和正方形AMNC,如图3,利用(3)中的结论求多边形DEMNFG的面积,直接写出结论.
相关试题

