【题目】(1)特例求解:在△ABC中,若三角形的三边为6、8、10,则这个三角形的面积 为 .
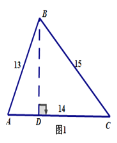
(2)一般化探究:在三角形ABC中,若AB=13,AC=14,BC=15,求△ABC的面积.
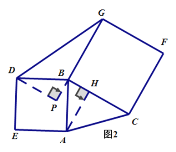
(3)模型建立:在图1三角形中,分别以AB,BC为边向外作正方形ABDE和正方形BCFG,试说明S△ABC=S△BDG.(温馨提示:作DP![]() BG,AH
BG,AH![]() BC)
BC)
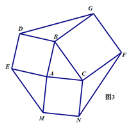
(4)模型应用:分别以图1中三角形的三边为边向外作正方形ABDE、正方形BCFG和正方形AMNC,如图3,利用(3)中的结论求多边形DEMNFG的面积,直接写出结论.
参考答案:
【答案】(1)24;(2)84;(3)见解析;(4)926.
【解析】
(1)先用勾股定理的逆定理判断三角形为直角三角形,再直接直角三角形面积公式求解;
(2)通过作一边上的高将一般三角形转化为直角三角形,利用勾股定理建立方程组计算,即可求解;
(3)先证明![]() ≌
≌![]() (AAS)得到DP=AH,再利用等底等高的三角形面积相等即可得证;
(AAS)得到DP=AH,再利用等底等高的三角形面积相等即可得证;
(4)利用(3)的结论得到![]() =
=![]() =
=![]() =
=![]() ,再结合正方形的面积公式得到多边形DEMNFG的面积=4
,再结合正方形的面积公式得到多边形DEMNFG的面积=4![]() +
+![]() +
+![]() +
+![]() ,从而得解.
,从而得解.
解:(1)∵![]() ,∴△ABC为直角三角形,∴
,∴△ABC为直角三角形,∴![]() ;
;
(2)如图

过点B作BD⊥AC交AC于D,
设AD=x,则DC=14-x,由勾股定理可得:
在直角三角形ADB中,![]() ,
,
在直角三角形BCD中,![]() ,
,
∴![]() ,
,
解得:x=5,
∴![]() ,
,
∴BD=12,
∴![]() ;
;
(3)如图

分别过点D、A作DP![]() BG,AH
BG,AH![]() BC交GB的延长线与P,交BC与H,
BC交GB的延长线与P,交BC与H,
∵∠DBA+∠ABC+∠CBG+∠DBG=360°,而∠DBA=∠CBG=90°,
∴∠ABC+∠DBG=180°,
又∵∠DBP+∠DBG=180°,
∴∠ABC=∠DBP,
在![]() 和
和![]() 中
中

∴![]() ≌
≌![]() (AAS),
(AAS),
∴DP=AH,
又∵![]() ,
,
![]() ,
,
而BC=BG,DP=AH,
∴![]() =
=![]() ;
;
(4)如图

由(3)的证明方法及结论可得:![]() =
=![]() =
=![]() =
=![]() ,
,
而![]() ,
,![]() ,
,![]() ,,
,,
∴多边形DEMNFG的面积=![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]()
=4![]() +
+![]() +
+![]() +
+![]() ,
,
=4×84+![]() +
+![]() +
+![]()
=926
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线L:
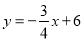 与
与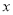 轴、
轴、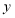 轴分别交于
轴分别交于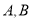 两点,在y轴上有一点
两点,在y轴上有一点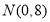 ,动点M从A点出发以每秒1个单位的速度沿射线AO匀速运动.
,动点M从A点出发以每秒1个单位的速度沿射线AO匀速运动.(1)点A的坐标: ;点B的坐标: ;
(2)求△NOM的面积S与M的移动时间t之间的函数关系式;
(3)当
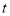 为何值时,
为何值时,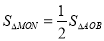 ,求出此时点M的坐标;
,求出此时点M的坐标;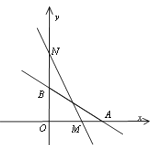
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次根式的化简中,若被开方数还有根号,有的能将被开方数化成另一个二次根式的平方的形式,比如:
 ,聪明的你可以继续探究,当a,b,m,n为正整数时,若
,聪明的你可以继续探究,当a,b,m,n为正整数时,若 ,则有
,则有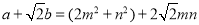 ,所以
,所以 .模仿上述探究解决下列问题:
.模仿上述探究解决下列问题:(1)当a,b,m,n为正整数时,
 ,请用含m,n的代数式分别表示a,b:a= ,b= .
,请用含m,n的代数式分别表示a,b:a= ,b= .(2)填空:
 =( +
=( +  )2
)2(3)若
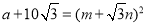 ,且a,m,n均为正整数,求a的值.
,且a,m,n均为正整数,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】有下列命题:①两条直线被第三条直线所截,同位角相等;②0.1的算术平方根是0.01;③算术平方根等于它本身的数是1;④如果点P(3-2n,1)到两坐标轴的距离相等,则n=1;⑤若a2=b2,则a=b;⑥若
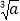 =
=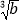 ,则a=b.其中假命题的个数是( )
,则a=b.其中假命题的个数是( )A. 3个B. 4个C. 5个D. 6个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间 每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂加工一批零件,为了提高工人工作积极性,工厂规定每名工人每天薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的( )
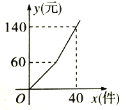
A.a=20
B.b=4
C.若工人甲一天获得薪金180元,则他共生产45件.
D.人乙一天生产40(件),则他获得薪金140元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=115°,∠ACF=25°,则∠FEC=_____.

相关试题

