【题目】某校八年级生物兴趣小组租两艘快艇去微山湖生物考察,他们从同一码头出发,第一艘快艇沿北偏西70°方向航行50千米,第二艘快艇沿南偏西20°方向航行50千米,如果此时第一艘快艇不动,第二艘快艇向第一艘快艇靠拢,那么第二艘快艇航行的方向和距离分别是( )
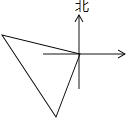
A. 南偏东![]() ,
,![]() 千米 B. 北偏西
千米 B. 北偏西![]() ,
,![]() 千米
千米
C. 南偏东![]() ,100千米 D. 北偏西
,100千米 D. 北偏西![]() ,100千米
,100千米
参考答案:
【答案】B
【解析】
根据题意得出AO=BO以及∠BOA=90°,进而得出第二艘快艇航行的方向和距离.
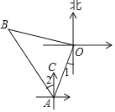
解:∵第一艘快艇沿北偏西70°方向,第二艘快艇沿南偏西20°方向,
∴∠BOA=90°,
∵BO=AO=50km,
∴AB=![]() km,∠B=∠OAB=45°,
km,∠B=∠OAB=45°,
∵第二艘快艇沿南偏西20°方向,
∴∠1=∠CAO=20°,
∴∠2=45°20°=25°,
∴第二艘快艇航行的方向和距离分别是:北偏西25°,![]() 千米.
千米.
故答案选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B是函数y=
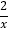 的图象上关于原点对称的任意两点,BC∥x轴,AC∥y轴,△ABC的面积记为S,则S= .
的图象上关于原点对称的任意两点,BC∥x轴,AC∥y轴,△ABC的面积记为S,则S= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
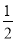 x与双曲线y=
x与双曲线y=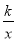 (k>0)交于A、B两点,且点A的横坐标为4.
(k>0)交于A、B两点,且点A的横坐标为4.(1)求k的值;
(2)若双曲线y=
 (k>0)上一点C的纵坐标为8,求△AOC的面积.
(k>0)上一点C的纵坐标为8,求△AOC的面积.
-
科目: 来源: 题型:
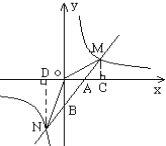
查看答案和解析>>【题目】如图,已知反比例函数
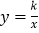 的图象与一次函数y=ax+b的图象交于M(2,m)和N(-1,-4)两点.
的图象与一次函数y=ax+b的图象交于M(2,m)和N(-1,-4)两点.(1)求这两个函数的解析式;
(2)求△MON的面积;
(3)请判断点P(4,1)是否在这个反比例函数的图象上,并说明理由.
(4)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:①所有锐角三角函数值都为正数;②解直角三角形时只需已知除直角外的两个元素;③Rt△ABC中,∠B=90°,则sin2A+cos2A=1;④Rt△ABC中,∠A=90°,则tanCsinC=cosC.其中正确的命题有( )
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB,BC是⊙O的弦,∠B=60°,点O在∠B内,点D为
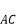 上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为2,则PN+MN的长度的最大值是( )
上的动点,点M,N,P分别是AD,DC,CB的中点.若⊙O的半径为2,则PN+MN的长度的最大值是( )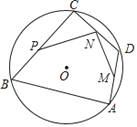
A.
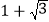
B.
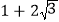
C.

D.
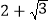
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形OABC的一边OA在x轴的负半轴上,O是坐标原点,tan∠AOC=
 ,反比例函数y=
,反比例函数y= 的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.
的图象经过点C,与AB交于点D,若△COD的面积为20,则k的值等于_____.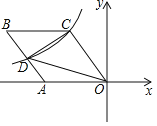
相关试题

