搜索
【题目】下列命题：①所有锐角三角函数值都为正数；②解直角三角形时只需已知除直角外的两个元素；③Rt△ABC中，∠B=90°，则sin2A+cos2A=1；④Rt△ABC中，∠A=90°，则tanCsinC=cosC．其中正确的命题有（ ）
A. 0个 B. 1个 C. 2个 D. 3个
参考答案：
【答案】C
【解析】
根据锐角三角函数的定义判断所有的锐角三角函数值都是正数；根据锐角三角函数的概念结合勾股定理可以证明sin2A+cos2A=1，tanCsinC=cosC．
①根据锐角三角函数的定义知所有的锐角三角函数值都是正数，故正确；
②两个元素中，至少得有一条边，故错误；
③根据锐角三角函数的概念，以及勾股定理，得则
=
=1，故正确；
④根据锐角三角函数的概念，得tanC=
，sinC=
，cosC=
，则tanCcosC=sinC，故错误．
故选C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y=kx+b的图象与反比例函数y=
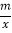的图象交于点A﹙﹣2，﹣5﹚，C﹙5，n﹚，交y轴于点B，交x轴于点D.（1）求反比例函数y=
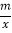和一次函数y=kx+b的表达式；（2）连接OA，OC.求△AOC的面积.
（3）当kx+b＞
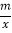时，请写出自变量x的取值范围.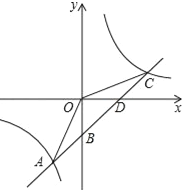
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线l1：y＝kx+b与x轴、y轴分别交于A，B两点，其中点B的坐标为（0，6），∠BAO=30°将直线l1沿着y轴正方向平移一段距离得到直线l2交y轴于点M，且l1与l2之间的距离为3，点C（x，y）是直线11上的一个动点，过点C作AB的垂线CD交y轴于点D．
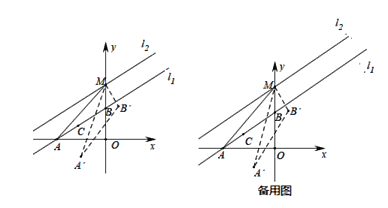
（1）求点M的坐标和直线l1的解析式；
（2）当C运动到什么位置时，△AOD的面积为21
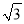，求出此时点C的坐标；（3）连接AM，将△ABM绕着点M旋转得到△A'B'M，在平面内是否存在一点N．使四边形AMA'N为矩形？若存在，求出点N的坐标：若不存在，请说明理由．
-
科目： 来源： 题型：
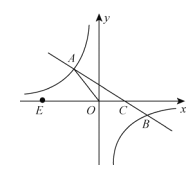
查看答案和解析>>【题目】如图，在平面直角坐标系xoy中，一次函数y=kx+b（k≠0）的图象与反比例函数
（m≠0）的图象交于二、四象限内的A、B两点，与x轴交于C点，点B的坐标为（6，n）。线段OA=5，E为x轴上一点，且
.(1)求该反比例函数和一次函数的解析式；
(2)求△AOC的面积；
(3)直接写出一次函数值大于反比例函数自变量x的取值范围。
-
科目： 来源： 题型：
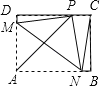
查看答案和解析>>【题目】如图，在长方形纸片ABCD中，AB＝12厘米，折叠纸片，使得点A落在CD边上的点P处，折痕为MN，点M、N分别在边AD、AB上，当点P恰好是CD边的中点时，点N与点B重合，若在折叠过程中NP＝NC，则PD＝_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,一艘海轮位于灯塔P的北偏东方向55°,距离灯塔为2海里的点A处.如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长是( )
A. 2海里 B. 2sin 55°海里
C. 2cos 55°海里 D. 2tan 55°海里
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一块形如四边形ABCD的草地中，AB＝3m，BC＝4m，CD＝12m，DA＝13m，且∠ABC＝90°，要以AC、CD、DA为边制作围栏，问围栏长多少米，草地面积多大？
相关试题
