【题目】如图,直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0)交于A、B两点,且点A的横坐标为4.
(k>0)交于A、B两点,且点A的横坐标为4.
(1)求k的值;
(2)若双曲线y=![]() (k>0)上一点C的纵坐标为8,求△AOC的面积.
(k>0)上一点C的纵坐标为8,求△AOC的面积.

参考答案:
【答案】(1)8;(2)15.
【解析】分析:(1)根据正比例函数先求出点A的坐标,从而求出了k值为8;
(2)根据k的几何意义可知![]() ,所以
,所以![]() .
.
本题解析:
解:(1)∵点A的横坐标为4,点A在直线y=![]() x上,
x上,
∴点A的纵坐标为y=![]() ×4=2,即A(4,2).
×4=2,即A(4,2).
又∵点A(4,2)在双曲线y=![]() 上,
上,
∴k=2×4=8.
(2)∵点C在双曲线y=![]() 上,且点C纵坐标为8,∴C(1,8).
上,且点C纵坐标为8,∴C(1,8).
如图,过点C作CM⊥x轴于M,过点A作AN⊥x轴于N.
∵S△COM=S△AON=![]() =4,
=4,
∴S△AOC=S四边形CMNA=![]() ×(|yA|+|yC|)×(|xA|-|xc|)=15.
×(|yA|+|yC|)×(|xA|-|xc|)=15.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数的图象经过点A(2,1),B(﹣1,﹣3).
(1)求此一次函数的解析式;
(2)求此一次函数的图象与x轴、y轴的交点坐标;
(3)求此一次函数的图象与两坐标轴所围成的三角形面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育课上,全班男同学进行了100米测验,达标成绩为15秒,如表是某小组8名男生的成绩记录,其中“
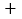 “表示成绩大于15秒.
“表示成绩大于15秒. 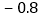
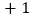
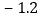
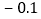
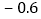
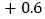
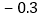
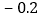
问:
 这个小组男生最优秀的成绩是多少秒?最差的成绩是多少秒?
这个小组男生最优秀的成绩是多少秒?最差的成绩是多少秒? 这个小组男生的达标率为多少?
这个小组男生的达标率为多少? 达标率
达标率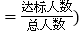
 这个小组男生的平均成绩是多少秒?
这个小组男生的平均成绩是多少秒? -
科目: 来源: 题型:
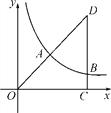
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,Rt△OCD的一边OC在x轴上,∠C=90°,点D在第一象限,OC=3,DC=4,反比例函数的图象经过OD的中点A.
(1)求该反比例函数的表达式;
(2)若该反比例函数的图象与Rt△OCD的另一边DC交于点B,求过A、B两点的直线的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种商品的标准价格是200元,但随着季节的变化,商品的价格可浮动
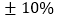 ,想一想.
,想一想. 的含义是什么?
的含义是什么?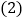 请你计算出该商品的最高价格和最低价格;
请你计算出该商品的最高价格和最低价格; 如果以标准价为标准,超过标准价记“
如果以标准价为标准,超过标准价记“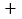 ”,低于标准价记“
”,低于标准价记“ ”,该商品价格的浮动范围又可以怎样表示?
”,该商品价格的浮动范围又可以怎样表示? -
科目: 来源: 题型:
查看答案和解析>>【题目】向阳花卉基地出售两种花卉——百合和玫瑰,其单价为玫瑰4元/株、百合5元/株,如果同一客户所购的玫瑰数量大于1 200株,那么每株玫瑰还可降价1元.现某鲜花店向向阳花卉基地采购玫瑰1 000~1 500株、百合若干株,恰好花去了9 000元,然后再以玫瑰5元/株、百合6.5元/株的价格卖出.问:此鲜花店应如何采购这两种鲜花才能使获得的毛利润最大?(注:1 000~1 500株,表示大于或等于1 000株,且小于或等于1 500株,毛利润=鲜花店卖出百合和玫瑰所获的总金额—购进百合和玫瑰所需的总金额)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在矩形ABCD中,AB=10 cm,BC=8 cm.点P从点A出发,沿A→B→C→D的路线运动,到点D停止;点Q从点D出发,沿D→C→B→A的路线运动,到点A停止.若点P、点Q同时出发,点P的速度为每秒1 cm,点Q的速度为每秒2 cm,a秒时,点P、点Q同时改变速度,点P的速度变为每秒b cm,点Q的速度变为每秒d cm.图②是点P出发x秒后△APD的面积S1(cm2)与时间x(秒)的函数关系图象;图③是点Q出发x秒后△AQD的面积S2(cm2)与时间x(秒)的函数关系图象.

(1)参照图②,求a、 b及图②中c的值;
(2)求d的值;
(3)设点P离开点A的路程为y1(cm),点Q到点A还需要走的路程为y2(cm),请分别写出改变速度后,y1、y2与出发后的运动时间x(秒)的函数关系式,并求出点P、点Q相遇时x的值;
(4)当点Q出发__ __秒时,点Q的运动路程为25 cm.
相关试题

