【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如:![]() ,则
,则![]() 是“和谐分式”.
是“和谐分式”.
(1)下列分式中,属于“和谐分式”的是_____(填序号);
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
(2)将“和谐分式”![]() 化成一个整式与一个分子为常数的分式的和的形式为:
化成一个整式与一个分子为常数的分式的和的形式为:![]() =_______(要写出变形过程);
=_______(要写出变形过程);
(3)应用:先化简![]() ,并求x取什么整数时,该式的值为整数.
,并求x取什么整数时,该式的值为整数.
参考答案:
【答案】(1)①③④ (2)a-1+![]() (3) x=-3
(3) x=-3
【解析】
(1)由“和谐分式”的定义对①③④变形即可得;
(2)由原式=![]() 可得;
可得;
(3)将原式变形为![]() ,据此得出x+1=±1或x+1=±2,即x=0或-2或1或-3,又x≠0、1、-1、-2,据此可得答案.
,据此得出x+1=±1或x+1=±2,即x=0或-2或1或-3,又x≠0、1、-1、-2,据此可得答案.
(1)①![]() ,是和谐分式;③
,是和谐分式;③![]() ,是和谐分式;④
,是和谐分式;④![]() ,是和谐分式;
,是和谐分式;
故答案为:①③④;
(2)![]()
![]() ,
,
故答案为:a-1、![]() ;
;
(3)原式=![]()
![]()
![]()
![]()
![]()
∴当x+1=±1或x+1=±2时,分式的值为整数
此时x=0或﹣2或1或﹣3
又∵分式有意义时x≠0、1、﹣1、﹣2,
∴x=﹣3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润 (元)与销售单价
(元)与销售单价  (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知用3辆A型车和2辆B型车一次可运货19吨;用2辆A型车和3辆B型车一次可运货 21吨.(每辆车每次都满载货物)
(1)求1辆A型车和1辆B型车载满货物一次分别可以运多少吨?
(2)某货物中心现有49吨货物,计划同时租用A型车和B型车若干辆,一次运完,且恰好每辆车都载满货物,请问有哪几种不同的租车方法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD.
(1)如图1,若∠A=35°,∠C=48°则∠E= °.
(2)如图2,若∠E=120°,∠C=110°,求∠A+∠F的度数;
(3)如图3,若∠E=110°,

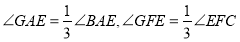 ,若GD∥FC,请直接写出∠AGF与∠GDC的数量关系: .
,若GD∥FC,请直接写出∠AGF与∠GDC的数量关系: .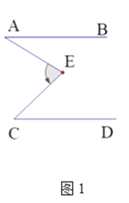


-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)

(2)-(a2b)3+2a2b(-3a2b)2
(3)

(4)

(5)(a+2b﹣c)(a﹣2b+c)
(6)2(m+1)2-(2m+1)(2m-1)
(7)
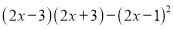
(8)用整式的乘法公式计算:

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
 分别交x轴、y轴于A、B两点.
分别交x轴、y轴于A、B两点.
(1)求A、B两点的坐标;
(2)设P是直线AB上一动点(点P与点A不重合),⊙P始终和x轴相切,和直线AB相交于C、D两点(点C的横坐标小于点D的横坐标).若P点的横坐标为m,试用含有m的代数式表示点C的横坐标;
(3)在(2)的条件下,若点C在线段AB上,当△BOC为等腰三角形时求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
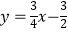 与抛物线
与抛物线 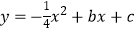 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.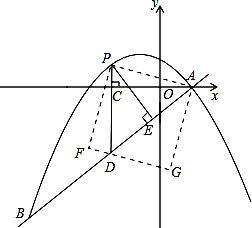
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为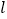 ,点P的横坐标为
,点P的横坐标为 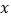 ,求
,求 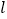 关于
关于 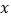 的函数关系式,并求出
的函数关系式,并求出 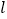 的最大值;
的最大值;
②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在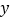 轴上时,求出对应点P的坐标.
轴上时,求出对应点P的坐标.
相关试题

