【题目】某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润 ![]() (元)与销售单价
(元)与销售单价 ![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大;(3)商场的营销部结合上述情况,提出了A、B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由.
参考答案:
【答案】
(1)解:由题意得,销售量= ![]() ,
,
则 ![]() ;
;
(2)解:方案A:由题可得 ![]() ,因为
,因为 ![]() ,对称轴为x=35,
,对称轴为x=35,
抛物线开口向下,在对称轴左侧, ![]() 随
随 ![]() 的增大而增大,
的增大而增大,
所以,当x=30时,w取最大值为2000元,
方案B:由题意得 ![]()
解得: ![]() ,
,
在对称轴右侧,w随x的增大而减小,
所以,当x=45时,w取最大值为1250元
因为2000元>1250元,
所以选择方案A.
【解析】(1)先求出上涨后的销售量,再根据利润=(销售单价-进价)×销售量,列出函数关系式即可。
(2)根据(1)式列出的函数关系式,运用配方法求最大值。
(3)分别求出方案A、B中x的取值范围,再根据二次函数的性质分别求出A、B方案的最大利润,然后进行比较。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费.某顾客刚好消费200元.
(1)该顾客至少可得到元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小丽假期在娱乐场游玩时,想要利用所学的数学知识测量某个娱乐场地所在山坡AE的高度.她先在山脚下的点E处测得山顶A的仰角是30°,然后,她沿着坡度i=1∶1的斜坡步行15分钟到达C处,此时,测得点A的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上,求出娱乐场地所在山坡AE的高度AB.(精确到0.1米,参考数据:
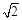 ≈1.41).
≈1.41).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中:①过一点有且只有一条直线与已知直线平行;②过一点有且只有一条直线与已知直线垂直;③垂直于同一直线的两条直线互相平行;④平行于同一直线的两条直线互相平行;⑤两条直线被第三条直线所截,如果同旁内角相等,那么这两条直线互相平行;⑥连结
 、
、 两点的线段就是
两点的线段就是 、
、 两点之间的距离,其中正确的有( )
两点之间的距离,其中正确的有( )A.
 个B.
个B. 个C.
个C. 个D.
个D. 个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知用3辆A型车和2辆B型车一次可运货19吨;用2辆A型车和3辆B型车一次可运货 21吨.(每辆车每次都满载货物)
(1)求1辆A型车和1辆B型车载满货物一次分别可以运多少吨?
(2)某货物中心现有49吨货物,计划同时租用A型车和B型车若干辆,一次运完,且恰好每辆车都载满货物,请问有哪几种不同的租车方法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD.
(1)如图1,若∠A=35°,∠C=48°则∠E= °.
(2)如图2,若∠E=120°,∠C=110°,求∠A+∠F的度数;
(3)如图3,若∠E=110°,

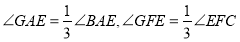 ,若GD∥FC,请直接写出∠AGF与∠GDC的数量关系: .
,若GD∥FC,请直接写出∠AGF与∠GDC的数量关系: .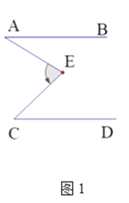


-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如:
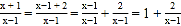 ,则
,则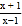 是“和谐分式”.
是“和谐分式”.(1)下列分式中,属于“和谐分式”的是_____(填序号);
①
 ;②
;②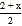 ;③
;③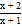 ;④
;④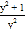 ;
;(2)将“和谐分式”
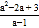 化成一个整式与一个分子为常数的分式的和的形式为:
化成一个整式与一个分子为常数的分式的和的形式为: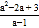 =_______(要写出变形过程);
=_______(要写出变形过程);(3)应用:先化简
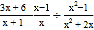 ,并求x取什么整数时,该式的值为整数.
,并求x取什么整数时,该式的值为整数.
相关试题

