【题目】如图,在平面直角坐标系中,直线 ![]() 与抛物线
与抛物线 ![]() 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.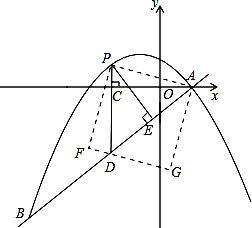
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为 ![]() ,点P的横坐标为
,点P的横坐标为 ![]() ,求
,求 ![]() 关于
关于 ![]() 的函数关系式,并求出
的函数关系式,并求出 ![]() 的最大值;
的最大值;
②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在 ![]() 轴上时,求出对应点P的坐标.
轴上时,求出对应点P的坐标.
参考答案:
【答案】
(1)解:对于 ![]() ,当y=0,x=2.当x=-8时,y=-
,当y=0,x=2.当x=-8时,y=- ![]() .
.
∴A点坐标为(2,0),B点坐标为(-8,- ![]() ).
).
由抛物线 ![]() 经过A、B两点,得
经过A、B两点,得 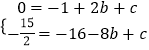 ,解得
,解得 ![]() ,
, ![]() .
.
∴ ![]() ;
;
(2)解:①设直线 ![]() 与y轴交于点M,
与y轴交于点M,
当x=0时,y= ![]() .∴OM=
.∴OM= ![]() .
.
∵点A的坐标为(2,0),∴OA=2.
∴AM= ![]() .
.
∴OM∶OA∶AM=3∶4∶5.
由题意得,∠PDE=∠OMA,∠AOM=∠PED=90°,
∴△AOM∽△PED.
∴DE∶PE∶PD=3∶4∶5.
∵点P是直线AB上方的抛物线上一动点,
∵PD⊥x轴,
∴PD两点横坐标相同,
∴PD=yP-yD= ![]() =
= ![]() ,
,
∴ ![]() .
.
∴x=-3时,l最大=15;

②当点G落在y轴上时,如图2,
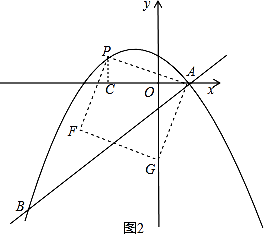
由△ACP≌△GOA得PC=AO=2,
即 ![]() ,解得x=
,解得x= ![]() ,
,
所以P1( ![]() ,2),P2(
,2),P2( ![]() ,2),
,2),
如图3,过点P作PN⊥y轴于点N,过点P作PS⊥x轴于点S,
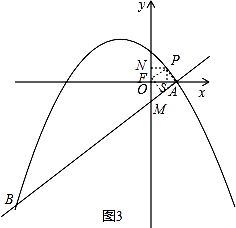
由△PNF≌△PSA,
PN=PS,可得P点横纵坐标相等,
故得当点F落在y轴上时, ![]() ,解得
,解得 ![]() ,
,
可得P3( ![]() ,
, ![]() ),
),
P4( ![]() ,
, ![]() ),(舍去).
),(舍去).
综上所述:满足题意的点P有三个,分别是P1( ![]() ,2),P2(
,2),P2( ![]() ,2),P3(
,2),P3( ![]() ,
, ![]() ).
).
【解析】(1)利用一次函数的解析式当y=0时求出点A的坐标,再将x=-8代入函数解析式求出B的坐标,再利用待定系数法求二次函数解析式解答。
(2)①设z直线AB与y轴交于点M,根据勾股定理求出AM长,及三边之比,再证明△AOM∽△PED.得出DE∶PE∶PD=3∶4∶5,由点P是直线AB上方的抛物线上一动点,PD⊥x轴,得出P、D两点横坐标相同,即可求出PD的长,再根据三角形的周长公式列式整理即可得解,再根据二次函数的最值问题解答。
②当点G在y轴上时,根据正方形的性质,先证△ACP≌△GOA,得PC=AO=2,根据二次函数的解析式建立方程求解,即可求出点P的坐标;
当点F在y轴上时,过点PM⊥x轴于M,作PN⊥y轴于N,根据正方形的性质,先证△PNF≌△PSA,得出PN=PS,可得P点横纵坐标相等,建立方程求解,即可求出点P的坐标。
【考点精析】利用二次函数的最值和正方形的性质对题目进行判断即可得到答案,需要熟知如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如:
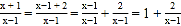 ,则
,则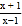 是“和谐分式”.
是“和谐分式”.(1)下列分式中,属于“和谐分式”的是_____(填序号);
①
 ;②
;②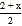 ;③
;③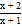 ;④
;④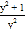 ;
;(2)将“和谐分式”
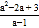 化成一个整式与一个分子为常数的分式的和的形式为:
化成一个整式与一个分子为常数的分式的和的形式为: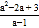 =_______(要写出变形过程);
=_______(要写出变形过程);(3)应用:先化简
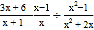 ,并求x取什么整数时,该式的值为整数.
,并求x取什么整数时,该式的值为整数. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)

(2)-(a2b)3+2a2b(-3a2b)2
(3)

(4)

(5)(a+2b﹣c)(a﹣2b+c)
(6)2(m+1)2-(2m+1)(2m-1)
(7)
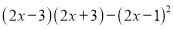
(8)用整式的乘法公式计算:

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
 分别交x轴、y轴于A、B两点.
分别交x轴、y轴于A、B两点.
(1)求A、B两点的坐标;
(2)设P是直线AB上一动点(点P与点A不重合),⊙P始终和x轴相切,和直线AB相交于C、D两点(点C的横坐标小于点D的横坐标).若P点的横坐标为m,试用含有m的代数式表示点C的横坐标;
(3)在(2)的条件下,若点C在线段AB上,当△BOC为等腰三角形时求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点A2 019的坐标为____________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】从甲地到乙地有两条公路,一条是全长600km的普通公路,另一条是全长480km的高速公路,某客车在高速公路上行驶的平均速度比在普通公路上快45
 /
/ ,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需的时间.
,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需的时间. -
科目: 来源: 题型:
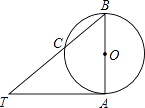
查看答案和解析>>【题目】如图,AB是⊙O的直径,TA切⊙O于点A,连结TB交⊙O于点C,∠BTA=40°,点M是圆上异于B,C的一个动点,则∠BMC的度数等于( )
A.50°
B.50°或130°
C.40°
D.40°或140°
相关试题

