【题目】有理数a、b在数轴上的对应点位置如图所示 ![]()
(1)用“<”连接0、﹣a、﹣b、﹣1
(2)化简:|a|﹣2|a+b﹣1|﹣ ![]() |b﹣a﹣1|
|b﹣a﹣1|
(3)若a2c+c<0,且c+b>0,求 ![]() +
+ ![]() ﹣
﹣ ![]() 的值.
的值.
参考答案:
【答案】
(1)解:∵a<﹣1<0<b<1,
∴﹣1<﹣b<0<﹣a
(2)解:由图可知:a<0,a+b﹣1<0,b﹣a﹣1>0
∴原式=﹣a﹣2(﹣a﹣b+1)﹣ ![]() (b﹣a﹣1)=
(b﹣a﹣1)= ![]() a+
a+ ![]() b﹣
b﹣ ![]()
(3)解:∵a2c+c<0
∴c<0
∵c+b>0
∴|c|<|b|
∴原式=1﹣1﹣(﹣1)=1
【解析】根据数轴即可比较大小,然后再化简.
【考点精析】根据题目的已知条件,利用数轴和绝对值的相关知识可以得到问题的答案,需要掌握数轴是规定了原点、正方向、单位长度的一条直线;正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;注意:绝对值的意义是数轴上表示某数的点离开原点的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.
【1】如图1,若点P在BC边上,此时PD=0,易证PD,PE,PF与AB满足的数量关系PD+PE+PF=AB;当点P在△ABC内,先在图2中作出图形,并写出PD,PE,PF与AB满足的数量关系,然后证明你的结论
【2】当点P在△ABC外,先在图3中作出图形,然后写出PD,PE,PF与AB满足的数量关系.(不用说明理由)

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)16+(﹣25)+24+(﹣35)
(2)(﹣ )×(﹣1
)×(﹣1  )÷(﹣2
)÷(﹣2  )
)
(3)23×(﹣5)﹣(﹣3)÷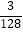
(4)|﹣10|+|(﹣4)2﹣(1﹣32)×2| -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程x2+3x﹣4=0的两根为x1、x2 , 则x12+x1x2+x22= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程没有实数根的是( )
A.x2=0B.x2+x=0C.x2+x+1=0D.x2+x﹣1=0
相关试题

