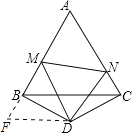
【题目】如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为 .

参考答案:
【答案】6.
【解析】
试题分析:∵△BDC是等腰三角形,且∠BDC=120°,∴∠BCD=∠DBC=30°,
∵△ABC是边长为3的等边三角形,∴∠ABC=∠BAC=∠BCA=60°,∴∠DBA=∠DCA=90°,
延长AB至F,使BF=CN,连接DF,
在Rt△BDF和Rt△CND中,BF=CN,DB=DC,∴△BDF≌△CND,∴∠BDF=∠CDN,DF=DN,
∵∠MDN=60°,∴∠BDM+∠CDN=60°,∴∠BDM+∠BDF=60°,∠FDM=60°=∠MDN,DM为公共边,
∴△DMN≌△DMF,∴MN=MF,
∴△AMN的周长是:AM+AN+MN=AM+MB+BF+AN=AB+AC=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列正整数中,属于素数的是( )
A.2B.4C.6D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.
【1】如图1,若点P在BC边上,此时PD=0,易证PD,PE,PF与AB满足的数量关系PD+PE+PF=AB;当点P在△ABC内,先在图2中作出图形,并写出PD,PE,PF与AB满足的数量关系,然后证明你的结论
【2】当点P在△ABC外,先在图3中作出图形,然后写出PD,PE,PF与AB满足的数量关系.(不用说明理由)

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)16+(﹣25)+24+(﹣35)
(2)(﹣ )×(﹣1
)×(﹣1  )÷(﹣2
)÷(﹣2  )
)
(3)23×(﹣5)﹣(﹣3)÷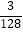
(4)|﹣10|+|(﹣4)2﹣(1﹣32)×2| -
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a、b在数轴上的对应点位置如图所示
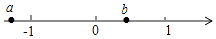
(1)用“<”连接0、﹣a、﹣b、﹣1
(2)化简:|a|﹣2|a+b﹣1|﹣ |b﹣a﹣1|
|b﹣a﹣1|
(3)若a2c+c<0,且c+b>0,求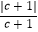 +
+ 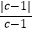 ﹣
﹣ 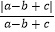 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程x2+3x﹣4=0的两根为x1、x2 , 则x12+x1x2+x22= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
相关试题

