【题目】计算:
(1)16+(﹣25)+24+(﹣35)
(2)(﹣ ![]() )×(﹣1
)×(﹣1 ![]() )÷(﹣2
)÷(﹣2 ![]() )
)
(3)23×(﹣5)﹣(﹣3)÷ ![]()
(4)|﹣10|+|(﹣4)2﹣(1﹣32)×2|
参考答案:
【答案】
(1)解:原式=﹣25﹣35+16+24=﹣60+40=﹣20
(2)解:原式=﹣ ![]() ×
× ![]() ×
× ![]() =﹣
=﹣ ![]()
(3)解:原式=﹣115+128=13
(4)解:原式=10+32=42
【解析】(1)原式结合后,相加即可得到结果;(2)原式从左到右依次计算即可得到结果;(3)原式先计算乘除运算,再计算加减运算即可得到结果;(4)原式先计算乘方运算,再计算乘法运算,最后算加减运算即可得到结果.
【考点精析】关于本题考查的有理数的四则混合运算,需要了解在没有括号的不同级运算中,先算乘方再算乘除,最后算加减才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:ab4﹣4ab3+4ab2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列正整数中,属于素数的是( )
A.2B.4C.6D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.
【1】如图1,若点P在BC边上,此时PD=0,易证PD,PE,PF与AB满足的数量关系PD+PE+PF=AB;当点P在△ABC内,先在图2中作出图形,并写出PD,PE,PF与AB满足的数量关系,然后证明你的结论
【2】当点P在△ABC外,先在图3中作出图形,然后写出PD,PE,PF与AB满足的数量关系.(不用说明理由)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN,则△AMN的周长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a、b在数轴上的对应点位置如图所示
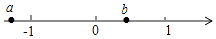
(1)用“<”连接0、﹣a、﹣b、﹣1
(2)化简:|a|﹣2|a+b﹣1|﹣ |b﹣a﹣1|
|b﹣a﹣1|
(3)若a2c+c<0,且c+b>0,求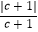 +
+ 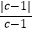 ﹣
﹣ 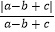 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程x2+3x﹣4=0的两根为x1、x2 , 则x12+x1x2+x22= .
相关试题

