搜索
【题目】下列方程没有实数根的是（ ）
A.x2＝0B.x2+x＝0C.x2+x+1＝0D.x2+x﹣1＝0
参考答案：
【答案】C
【解析】
分别计算出每个方程判别式的值，再进一步判断即可得出答案．
解：A．此方程判别式＝02﹣4×1×0＝0，故方程有两个相等的实数根；
B．此方程判别式＝12﹣4×1×0＝1＞0，故方程有两个不相等的实数根；
C．此方程判别式＝12﹣4×1×1＝﹣3＜0，故方程没有实数根；
D．此方程判别式＝02﹣4×1×(﹣1)＝5＞0，故方程有两个不相等的实数根；
故选：C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】有理数a、b在数轴上的对应点位置如图所示
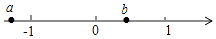
（1）用“＜”连接0、﹣a、﹣b、﹣1
（2）化简：|a|﹣2|a+b﹣1|﹣
|b﹣a﹣1|
（3）若a2c+c＜0，且c+b＞0，求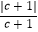
+ 
﹣ 
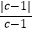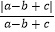的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知一元二次方程x2+3x﹣4=0的两根为x1、x2 ， 则x12+x1x2+x22= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（ ）
A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算（ab2）3的结果，正确的是（ ）
A.a3b6
B.a3b5
C.ab6
D.ab5 -
科目： 来源： 题型：
查看答案和解析>>【题目】最短路径问题：
例：如图所示，要在街道旁修建一个奶站，向居民区A、B提供牛奶，奶站应建在什么地方，才能使从A、B到它的距离之和最短．
解：只有A、C、B在一直线上时，才能使AC+BC最小．作点A关于直线“街道”的对称点A′，然后连接A′B，交“街道”于点C，则点C就是所求的点．
应用：已知：如图A是锐角∠MON内部任意一点，
在∠MON的两边OM，ON上各取一点B，C，组成三角形，使三角形周长最小.
（1）借助直角三角板在下图中找出符合条件的点B和C.
（2）若∠MON=30°，OA=10,求三角形的最小周长。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，已知A点从（1，0）点出发，以每秒1个单位长的速度沿着x轴的正方向运动，经过t秒后，以O、A为顶点作菱形OABC，使B．C点都在第一象限内，且AO=AC，又以P（0，
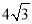）为圆心，PC为半径的圆恰好与OC所在的直线相切，则t=（ ）.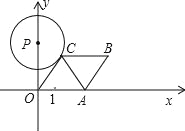
A．
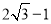B．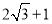
C．5 D．7
相关试题
