【题目】为了推动课堂教学改革,打造“高效课堂”,我市某中学对该校八年级部分学生就一学期以来“分组合作学习”方式的支持程度进行调查,统计情况如图,请根据图中提供的信息,回答下列问题:
(1)本次调查的八年级部分学生共有______名;请补全条形统计图;
(2)若该校八年级学生共有540人,请你估计该校八年级有多少名学生支持“分组合作学习”方式(含“非常喜欢”和“喜欢”两种情况的学生)?

参考答案:
【答案】(1)本次调查的总人数是54人;
(2)有160名学生支持“分组合作学习”方式.
【解析】试题分析:(1)喜欢的所占的扇形的圆心角的度数是120度,则所占的比例是![]() ,然后根据喜欢的人数是18人,据此即可求得总人数;利用总人数乘以非常喜欢的所占的比例即可求得人数,从而补全条形统计图;
,然后根据喜欢的人数是18人,据此即可求得总人数;利用总人数乘以非常喜欢的所占的比例即可求得人数,从而补全条形统计图;
(2)利用扇形图得出支持“分组合作学习”方式所占的百分比,利用样本估计总体即可.
试题解析:(1)本次调查的总人数是:18÷![]() =54(人);
=54(人);
非常喜欢的人数是:54×![]() =30(人),
=30(人),
如图所示:
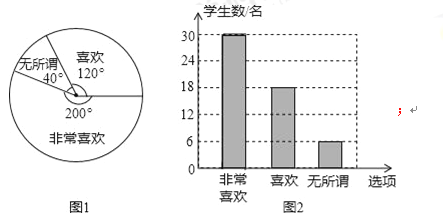
(2)∵“非常喜欢”和“喜欢”两种情况在扇形统计图中所占圆心角为:120°+200°=320°,
∴支持“分组合作学习”方式所占百分比为:![]() ×100%,
×100%,
∴该校八年级学生共有180人,有180×![]() =160名学生支持“分组合作学习”方式.
=160名学生支持“分组合作学习”方式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),点
 为线段
为线段 上一点,过点
上一点,过点 作射线
作射线 ,使
,使 ,将一直角三角板的直角顶点放在点
,将一直角三角板的直角顶点放在点 处,一边
处,一边 在射线
在射线 上,另一边
上,另一边 在线段
在线段 的下方.
的下方.(1)将图(1)中的直角三角板绕点
 按逆时针方向旋转,使
按逆时针方向旋转,使 落在射线
落在射线 上(如图(2)),则三角板旋转的角度为____度;
上(如图(2)),则三角板旋转的角度为____度;(2)继续将图2中的直角三角板绕点
 按逆时针方向旋转,使
按逆时针方向旋转,使 在
在 的内部(如图3).试求
的内部(如图3).试求 与
与 度数的差;
度数的差;(3)若图1中的直角三角板绕点
 按逆时针方向旋转一周,在此过程中:
按逆时针方向旋转一周,在此过程中:①当直角边
 所在直线恰好垂直于
所在直线恰好垂直于 时,
时,  的度数是________;
的度数是________;②设直角三角板绕点
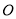 按每秒
按每秒 的速度旋转,当直角边
的速度旋转,当直角边 所在直线恰好平分
所在直线恰好平分 时,求三角板绕点
时,求三角板绕点 旋转时间
旋转时间 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某部队将在指定山区进行军事演习,为了使道路便于部队重型车辆通过,部队工兵连接到抢修一段长3600米道路的任务,按原计划完成总任务的
 后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.(1)按原计划完成总任务的
 时,已抢修道路 米;
时,已抢修道路 米;(2)求原计划每小时抢修道路多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
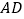 、
、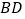 、
、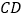 分别平分
分别平分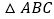 的外角
的外角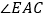 、内角
、内角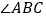 、外角
、外角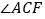 .以下结论:①
.以下结论:①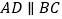 :②
:②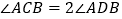 :③
:③ :④
:④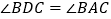 .其中正确的结论有( )
.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料并解答问题:
我们知道
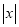 的几何意义是在数轴上数
的几何意义是在数轴上数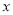 对应的点与原点的距离:
对应的点与原点的距离: 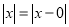 ,也就是说,
,也就是说, 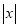 表示在数轴上数
表示在数轴上数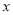 与数0对应点之间的距离;
与数0对应点之间的距离;这个结论可以推广为
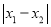 表示在数轴上数
表示在数轴上数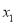 和数
和数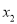 对应的点之间的距离;
对应的点之间的距离;例1解方程
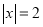 ,容易看出,在数轴上与原点距离为2的点对应的数为
,容易看出,在数轴上与原点距离为2的点对应的数为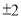 ,即该方程的解为
,即该方程的解为 .
.例2解不等式
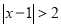 ,如图,在数轴上找出
,如图,在数轴上找出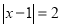 的解,即到1的距离为2的点对应的数为
的解,即到1的距离为2的点对应的数为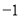 ,3,则
,3,则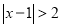 的解集为
的解集为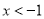 或
或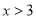 .
.
例3解方程
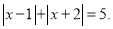 由绝对值的几何意义知,该方程表示求在数轴上与1和
由绝对值的几何意义知,该方程表示求在数轴上与1和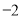 的距离之和为5的对应的
的距离之和为5的对应的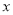 的值.在数轴上,1和
的值.在数轴上,1和 的距离为3,满足方程的
的距离为3,满足方程的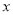 对应的点在1的右边或
对应的点在1的右边或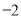 的左边,若
的左边,若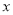 对应的点在1的右边,由下图可以看出
对应的点在1的右边,由下图可以看出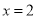 ;同理,若
;同理,若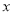 对应的点在
对应的点在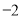 的左边,可得
的左边,可得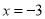 ,故原方程的解是
,故原方程的解是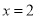 或
或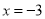 .
.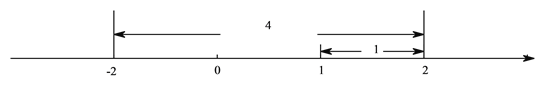
回答问题:(只需直接写出答案)
①解方程

②解不等式
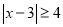
③解方程
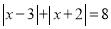
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
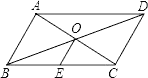
A. OE=
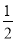 DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(
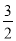 ,0),B(0,2),则点B2016的坐标为______________.
,0),B(0,2),则点B2016的坐标为______________.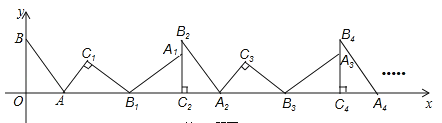
相关试题

