【题目】已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )
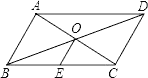
A. OE=![]() DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
参考答案:
【答案】D
【解析】由平行四边形的性质和三角形中位线定理得出选项A、B、C正确;由OB≠OC,得出∠OBE≠∠OCE,选项D错误;即可得出结论.
解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AB∥DC,
又∵点E是BC的中点,
∴OE是△BCD的中位线,
∴OE=![]() DC,OE∥DC,
DC,OE∥DC,
∴OE∥AB,
∴∠BOE=∠OBA,
∴选项A、B、C正确;
∵OB≠OC,
∴∠OBE≠∠OCE,
∴选项D错误;
故选D.
“点睛”此题考查了平行四边形的性质,还考查了三角形中位线定理,解决问题的方法是采用排除法解答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
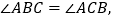
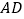 、
、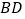 、
、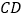 分别平分
分别平分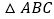 的外角
的外角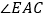 、内角
、内角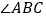 、外角
、外角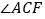 .以下结论:①
.以下结论:①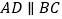 :②
:②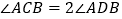 :③
:③ :④
:④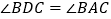 .其中正确的结论有( )
.其中正确的结论有( )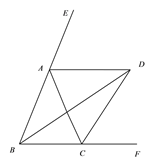
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了推动课堂教学改革,打造“高效课堂”,我市某中学对该校八年级部分学生就一学期以来“分组合作学习”方式的支持程度进行调查,统计情况如图,请根据图中提供的信息,回答下列问题:
(1)本次调查的八年级部分学生共有______名;请补全条形统计图;
(2)若该校八年级学生共有540人,请你估计该校八年级有多少名学生支持“分组合作学习”方式(含“非常喜欢”和“喜欢”两种情况的学生)?

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料并解答问题:
我们知道
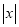 的几何意义是在数轴上数
的几何意义是在数轴上数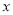 对应的点与原点的距离:
对应的点与原点的距离: 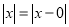 ,也就是说,
,也就是说, 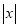 表示在数轴上数
表示在数轴上数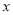 与数0对应点之间的距离;
与数0对应点之间的距离;这个结论可以推广为
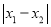 表示在数轴上数
表示在数轴上数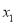 和数
和数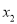 对应的点之间的距离;
对应的点之间的距离;例1解方程
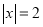 ,容易看出,在数轴上与原点距离为2的点对应的数为
,容易看出,在数轴上与原点距离为2的点对应的数为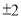 ,即该方程的解为
,即该方程的解为 .
.例2解不等式
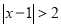 ,如图,在数轴上找出
,如图,在数轴上找出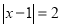 的解,即到1的距离为2的点对应的数为
的解,即到1的距离为2的点对应的数为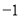 ,3,则
,3,则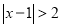 的解集为
的解集为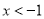 或
或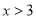 .
.
例3解方程
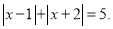 由绝对值的几何意义知,该方程表示求在数轴上与1和
由绝对值的几何意义知,该方程表示求在数轴上与1和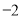 的距离之和为5的对应的
的距离之和为5的对应的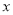 的值.在数轴上,1和
的值.在数轴上,1和 的距离为3,满足方程的
的距离为3,满足方程的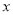 对应的点在1的右边或
对应的点在1的右边或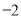 的左边,若
的左边,若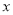 对应的点在1的右边,由下图可以看出
对应的点在1的右边,由下图可以看出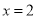 ;同理,若
;同理,若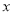 对应的点在
对应的点在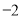 的左边,可得
的左边,可得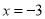 ,故原方程的解是
,故原方程的解是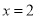 或
或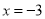 .
.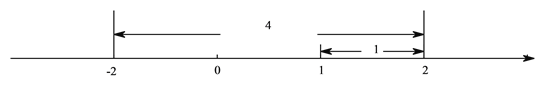
回答问题:(只需直接写出答案)
①解方程

②解不等式
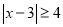
③解方程
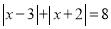
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(
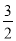 ,0),B(0,2),则点B2016的坐标为______________.
,0),B(0,2),则点B2016的坐标为______________.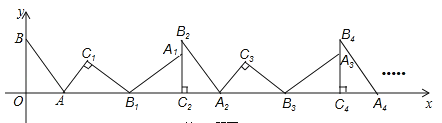
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多边形的某些边向两方延长,其他各边若不全在延长所得直线的同侧,则把这样的多边形叫做凹多边形.如图①五边形
 中,作直线
中,作直线 ,则边
,则边 、
、 分别在直线
分别在直线 的两侧,所以五边形
的两侧,所以五边形 就是一个凹五边形.我们简单研究凹多边形的边和角的性质.
就是一个凹五边形.我们简单研究凹多边形的边和角的性质.
(1)如图②,在凹六边形
 中,探索
中,探索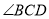 与
与 、
、 、
、 、
、 、
、 、之间的关系;
、之间的关系;(2)如图③,在凹四边形
 中,证明
中,证明 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在比例尺1∶8000000的地图上,量得太原到北京的距离为6.4厘米,则太原到北京的实际距离为 公里。
相关试题

