Question

【题目】如图，在△ABC中，∠A＝70°，∠B＝90°，点A关于BC的对称点是A'，点B关于AC的对称点是B'，点C关于AB的对称点是C'，若△ABC的面积是1，则△A'B'C'的面积是（　　）

A.2B.3C.4D.5

Answer 1

【答案】B

【解析】

BB′的延长线交A′C′于E，如图，根据轴对称的性质得到DB′=DB，BB′⊥AC，BC=BC′，AB=A′B，则可判断△ABC≌△A′BC′，所以∠C=∠A′C′B，AC=A′C′，则AC∥A′C′，所以DE⊥A′C′，且BD=BE，即B′E=3BD，然后利用三角形面积公式可得到S△A′B′C′=3S△ABC．

BB′的延长线交A′C′于E，如图，

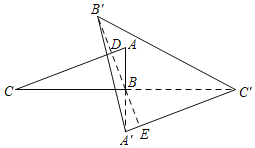
∵点B关于AC的对称点是B'，

∴DB′＝DB，BB′⊥AC，

∵点C关于AB的对称点是C'，

∴BC＝BC′，

∵点A关于BC的对称点是A'，

∴AB＝A′B，

而∠ABC＝∠A′BC′，

∴△ABC≌△A′BC′（SAS），

∴∠C＝∠A′C′B，AC＝A′C′，

∴AC∥A′C′，

∴DE⊥A′C′，

而△ABC≌△A′BC′，

∴BD＝BE，

∴B′E＝3BD，

∴S△A′B′C′＝A′C′×B′E＝3××BD×AC＝3S△ABC＝3×1＝3．

故选：B．