【题目】将下列推理过程填写完整. 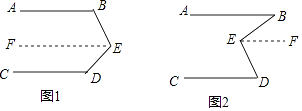
(1)如图1,已知∠B+∠BED+∠D=360°,求证AB∥CD. 证明:过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行)
∵EF∥CD,
∴∠D+∠DEF=180°,()
∵∠B+∠BED+∠D=360°,(已知)
∴∠B+∠BEF=∠B+∠BED+∠D﹣(∠D+∠DEF)=360°﹣180°=180°
∴EF∥AB,()
∴∥ , (平行于同一直线的两直线平行)
(2)如图2,已知∠BED=∠B+∠D,求证AB∥CD. 证明:过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行)
∵EF∥CD,
∴∠D=∠FED,()
∵∠BED=∠B+∠D(已知)
∴∠B=∠BEF﹣∠D=∠BED﹣∠FED=∠BEF,
∴∥ , ()
∴∥ . (平行于同一直线的两直线平行)
参考答案:
【答案】
(1)两直线平行,同旁内角互补;同旁内角互补,两直线平行;AB;CD
(2)两直线平行,内错角相等;AB;EF;内错角相等,两直线平行;AB;CD.
【解析】(1.)证明:过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行) ∵EF∥CD,
∴∠D+∠DEF=180°,( 两直线平行,同旁内角互补 )
∵∠B+∠BED+∠D=360°,( 已知 )
∴∠B+∠BEF=∠B+∠BED+∠D﹣(∠D+∠DEF )=360°﹣180°=180°,
∴EF∥AB,( 同旁内角互补,两直线平行 )
∴AB∥CD,( 平行于同一直线的两直线平行);
所以答案是:两直线平行,同旁内角互补;同旁内角互补,两直线平行;AB;CD;
(2.)证明:过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行)
∵EF∥CD,
∴∠D=∠FED,( 两直线平行,内错角相等 )
∵∠BED=∠B+∠D,(已知)
∴∠B=∠BED﹣∠D=∠BED﹣∠FED=∠BEF,
∴AB∥EF,( 内错角相等,两直线平行 )
∴AB∥CD,( 平行于同一直线的两直线平行).
所以答案是:两直线平行,内错角相等;AB;EF;内错角相等,两直线平行;AB;CD.
【考点精析】通过灵活运用平行公理和平行线的判定,掌握平行公理――平行线的存在性与惟一性;经过直线外一点,有且只有一条直线与这条直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行;同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是高线,CE是中线,DC=BE,DG⊥CE于点G,求证:
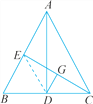
(1)G是CE的中点.
(2)∠B=2∠BCE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在实数范围内分解因式x3﹣4x的结果为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形的内角和是1800°,则这个多边形的边数是_______;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果│a│=4,b2=4,且a<b,那么a-b的值为( )
A. -6或-2 B. 6或2 C. -6或2 D. 6或-2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,M是边AB的中点,CH⊥AB于点H,CD平分∠ACB.

(1)求证:∠1=∠2.
(2)过点M作AB的垂线交CD的延长线于点E,连结AE,BE.求证:CM=EM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径AB的长为2,点C在圆周上,∠CAB=30°,点D是圆上一动点,DE∥AB交CA的延长线于点E,连接CD,交AB于点F.
(1)如图1,当∠ACD=45°时,求证:DE是⊙O的切线;
(2)如图2,当点F是CD的中点时,求△CDE的面积.

相关试题

