【题目】如果│a│=4,b2=4,且a<b,那么a-b的值为( )
A. -6或-2 B. 6或2 C. -6或2 D. 6或-2
参考答案:
【答案】A
【解析】
根据乘方法则、绝对值的性质求出a、b,根据题意确定a、b的值,根据有理数的加法法则计算即可.
∵|a|=4,b2=4,
∴a=±4,b=±2,
∵a<b,
∴a=-4,b=±2,
则a-b=-6或-2,
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在实数范围内分解因式x3﹣4x的结果为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形的内角和是1800°,则这个多边形的边数是_______;
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下列推理过程填写完整.
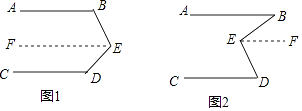
(1)如图1,已知∠B+∠BED+∠D=360°,求证AB∥CD. 证明:过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行)
∵EF∥CD,
∴∠D+∠DEF=180°,()
∵∠B+∠BED+∠D=360°,(已知)
∴∠B+∠BEF=∠B+∠BED+∠D﹣(∠D+∠DEF)=360°﹣180°=180°
∴EF∥AB,()
∴∥ , (平行于同一直线的两直线平行)
(2)如图2,已知∠BED=∠B+∠D,求证AB∥CD. 证明:过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行)
∵EF∥CD,
∴∠D=∠FED,()
∵∠BED=∠B+∠D(已知)
∴∠B=∠BEF﹣∠D=∠BED﹣∠FED=∠BEF,
∴∥ , ()
∴∥ . (平行于同一直线的两直线平行) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,M是边AB的中点,CH⊥AB于点H,CD平分∠ACB.

(1)求证:∠1=∠2.
(2)过点M作AB的垂线交CD的延长线于点E,连结AE,BE.求证:CM=EM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径AB的长为2,点C在圆周上,∠CAB=30°,点D是圆上一动点,DE∥AB交CA的延长线于点E,连接CD,交AB于点F.
(1)如图1,当∠ACD=45°时,求证:DE是⊙O的切线;
(2)如图2,当点F是CD的中点时,求△CDE的面积.

-
科目: 来源: 题型:
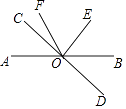
查看答案和解析>>【题目】如图,已知直线AB和CD相交于点O,∠COE=90°,OF平分∠AOE,∠COF=24°,求∠BOD的度数.
相关试题

