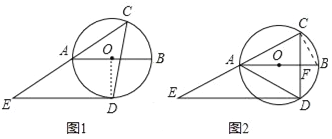
【题目】如图,⊙O的直径AB的长为2,点C在圆周上,∠CAB=30°,点D是圆上一动点,DE∥AB交CA的延长线于点E,连接CD,交AB于点F.
(1)如图1,当∠ACD=45°时,求证:DE是⊙O的切线;
(2)如图2,当点F是CD的中点时,求△CDE的面积.

参考答案:
【答案】(1)证明见解析;
(2)S△ECD=![]() EDCD=
EDCD=![]() .
.
【解析】
试题分析:(1)如图1中,连接OD,欲证明ED是切线,只要证明∠EDO=90°即可.
(2)如图2中,连接BC,利用勾股定理.以及直角三角形30度性质求出CD、DE即可.
试题解析:(1)如图1中,连接OD.
∵∠C=45°,
∴∠AOD=2∠C=90°,
∵ED∥AB,
∴∠AOD+∠EDO=180°,
∴∠EDO=90°,
∴ED⊥OD,
∴ED是⊙O切线.
(2)如图2中,连接BC,
∵CF=DF,
∴AF⊥CD,
∴AC=AD,
∴∠ACD=∠ADC,
∵AB∥ED,
∴ED⊥DC,
∴∠EDC=90°,
在RT△ACB中,∵∠ACB=90°,∠CAB=30°,AB=2,
∴BC=1,AC=![]() ,
,
∴CF=![]() AC=
AC=![]() ,CD=2CF=
,CD=2CF=![]() ,
,
在RT△ECD中,
∵∠EDC=90°,CD=![]() ,∠E=∠CAB=30°,
,∠E=∠CAB=30°,
∴EC=2CD=2![]() ,ED=
,ED= ![]() =3,
=3,
∴S△ECD= ![]() EDCD=
EDCD=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下列推理过程填写完整.
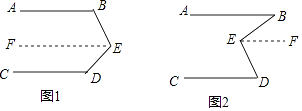
(1)如图1,已知∠B+∠BED+∠D=360°,求证AB∥CD. 证明:过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行)
∵EF∥CD,
∴∠D+∠DEF=180°,()
∵∠B+∠BED+∠D=360°,(已知)
∴∠B+∠BEF=∠B+∠BED+∠D﹣(∠D+∠DEF)=360°﹣180°=180°
∴EF∥AB,()
∴∥ , (平行于同一直线的两直线平行)
(2)如图2,已知∠BED=∠B+∠D,求证AB∥CD. 证明:过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行)
∵EF∥CD,
∴∠D=∠FED,()
∵∠BED=∠B+∠D(已知)
∴∠B=∠BEF﹣∠D=∠BED﹣∠FED=∠BEF,
∴∥ , ()
∴∥ . (平行于同一直线的两直线平行) -
科目: 来源: 题型:
查看答案和解析>>【题目】如果│a│=4,b2=4,且a<b,那么a-b的值为( )
A. -6或-2 B. 6或2 C. -6或2 D. 6或-2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,M是边AB的中点,CH⊥AB于点H,CD平分∠ACB.

(1)求证:∠1=∠2.
(2)过点M作AB的垂线交CD的延长线于点E,连结AE,BE.求证:CM=EM.
-
科目: 来源: 题型:
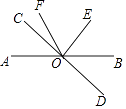
查看答案和解析>>【题目】如图,已知直线AB和CD相交于点O,∠COE=90°,OF平分∠AOE,∠COF=24°,求∠BOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+b的图象与反比例函数y=
 的图象相交于A,B两点,且交y轴于点C.已知点A(1,4),点B在第三象限,且点B的横坐标为t(t<﹣1).
的图象相交于A,B两点,且交y轴于点C.已知点A(1,4),点B在第三象限,且点B的横坐标为t(t<﹣1).(1)求反比例函数的解析式;
(2)用含t的式子表示k,b;
(3)若△AOB的面积为3,求点B的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A.a2+a3=a5
B.a3a4=a12
C.a6÷a3=a2
D.4a﹣a=3a
相关试题

