【题目】如图,在△ABC中,AD是高线,CE是中线,DC=BE,DG⊥CE于点G,求证:
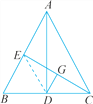
(1)G是CE的中点.
(2)∠B=2∠BCE.
参考答案:
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:
(1)如图,连接DE,由AD是△ABC的高,CE是△ABC的中线可证DE=![]() AB=BE,结合DC=BE可得DE=DC,由此可得△DEC是等腰三角形,由DG⊥CE可得G为CE的中点;
AB=BE,结合DC=BE可得DE=DC,由此可得△DEC是等腰三角形,由DG⊥CE可得G为CE的中点;
(2)由(1)的证明可知DE=DC,BE=DE,由此可得∠B=∠EDB,∠DEC=∠DCE,再由∠EDB=∠DEC+∠DCE可得结论.
试题解析:
(1)如图,连结DE.
∵AD是高线,
∴△ABD是直角三角形.
∵CE是AB边上的中线,
∴DE是Rt△ABD斜边上的中线.
∴DE=BE.
∵DC=BE,
∴DE=DC.
又∵DG⊥CE,
∴CG=EG,即G是CE的中点.
(2)∵DE=BE,
∴∠B=∠BDE.
∵DE=DC,
∴∠DEC=∠BCE.
∵∠BDE是△DCE的一个外角,
∴∠BDE=∠DEC+∠BCE=2∠BCE.
∴∠B=2∠BCE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
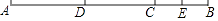
(1)如图,点C是线段AB上一点,D、E分别是AC、BC的中点,已知DE=6,求AB的长;
(2)若(1)中改为点C是射线AB上一点(不在线段AB上),其它条件不变,请画出图形,并直接写出相应的AB长. -
科目: 来源: 题型:
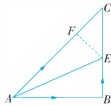
查看答案和解析>>【题目】如图,在Rt△ABC的场地上,∠B=90°,AB=BC,∠CAB的平分线AE交BC于点E.甲、乙两人同时从A处出发,以相同的速度分别沿AC和A→B→E线路前进,甲的目的地为C,乙的目的地为E.请你判断一下,甲、乙两人谁先到达各自的目的地?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下四组木棒中,哪一组的三条能够刚好做成直角三角形的木架( )
A. 7 cm,12 cm,15 cm B. 7 cm,12 cm,13 cm
C. 8 cm,15 cm,16 cm D. 3 cm,4 cm,5 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】在实数范围内分解因式x3﹣4x的结果为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形的内角和是1800°,则这个多边形的边数是_______;
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下列推理过程填写完整.
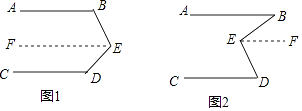
(1)如图1,已知∠B+∠BED+∠D=360°,求证AB∥CD. 证明:过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行)
∵EF∥CD,
∴∠D+∠DEF=180°,()
∵∠B+∠BED+∠D=360°,(已知)
∴∠B+∠BEF=∠B+∠BED+∠D﹣(∠D+∠DEF)=360°﹣180°=180°
∴EF∥AB,()
∴∥ , (平行于同一直线的两直线平行)
(2)如图2,已知∠BED=∠B+∠D,求证AB∥CD. 证明:过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行)
∵EF∥CD,
∴∠D=∠FED,()
∵∠BED=∠B+∠D(已知)
∴∠B=∠BEF﹣∠D=∠BED﹣∠FED=∠BEF,
∴∥ , ()
∴∥ . (平行于同一直线的两直线平行)
相关试题

