【题目】探索与运用:
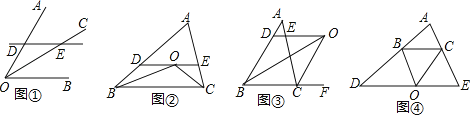
(1)基本图形:如图①,已知OC是∠AOB的角平分线,DE∥OB,分别交OA、OC于点D、E.求证:DE=OD;
(2)在图②中找出这样的基本图形,并利用(1)中的规律解决这个问题:已知△ABC中,两个内角∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,交AB、AC于点D、E.求证:DE=BD+CE;
(3)若将图②中两个内角的角平分线改为一个内角(如图③,∠ABC)、一个外角(∠ACF)和两个都是外角(如图④∠DBC、∠BCE)的角平分线,其它条件不变,则线段DE、BD、CE的数量关系分别是:图③为 、图④为 :并从中任选一个结论证明.
参考答案:
【答案】(1)(2)(3)证明见解析
【解析】
试题分析:(1)根据角平分线的定义得到∠AOC=∠BOC,根据平行线的性质得到∠DEO=∠BOC,等量代换得到∠DEO=AOC,根据等腰三角形的判定即可得到结论;
(2)根据△ABC中,∠ABC和∠ACB的平分线相交于点O.求证∠DBO=∠OBC,∠ECO=∠BCO,再利用两直线平行内错角相等,求证出∠DOB=∠DBO,∠COE=∠BCO,即BD=DO,OE=CE,然后利用等量代换即可求出结论;
(3)选③证明:由(1)中证明可得:DB=DO,EO=EC,根据线段的和差即可得到结论
证明:(1)∵OC平分∠AOB,
∴∠AOC=∠BOC,
∵DE∥OB,
∴∠DEO=∠BOC,
∴∠DEO=AOC,
∴DE=OD;
(2)∵∠ABC和∠ACB的平分线相交于点O,
∴∠DBO=∠OBC,∠ECO=∠BCO,
∵DE∥BC,交AB于点D,交AC于点E.
∴∠DOB=∠DBO,∠COE=∠ECO,
∴BD=DO,OE=CE,
∴DE=BD+CE;
(3)图③:DE=BD﹣CE,图④:DE=BD+CE,
选③证明:
由(1)中证明可得:DB=DO,EO=EC,
∴DE=OD=OE=DB﹣CE.
故答案为:DE=BD﹣CE,DE=BD+CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,平方数的开平方运算可以直接求得,如
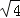 等,有些数则不能直接求得,如
等,有些数则不能直接求得,如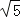 ,但可以通过计算器求得.还有一种方法可以通过一组数的内在联系,运用规律求得.请你观察下表:
,但可以通过计算器求得.还有一种方法可以通过一组数的内在联系,运用规律求得.请你观察下表:a … 0.04 4 400 40000 …
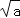 … x 2 y z …
… x 2 y z …(1)表格中的三个值分别为:x= ;y= ;z= ;
(2)用公式表示这一规律:当a=4×100n(n为整数)时,
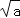 = ;
= ;(3)利用这一规律,解决下面的问题:
已知
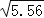 ≈2.358,则①
≈2.358,则①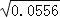 ≈ ;②
≈ ;②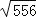 ≈ .
≈ . -
科目: 来源: 题型:
查看答案和解析>>【题目】下列多项式中是完全平方式的是( )
A. 2x2+4x-4 B. 16x2-8y2+1 C. 9a2-12a+4 D. x2y2+2xy+y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列判断不正确的是( )
A. 形状相同的图形是全等图形 B. 能够完全重合的两个三角形全等
C. 全等图形的形状和大小都相同 D. 全等三角形的对应角相等
-
科目: 来源: 题型:
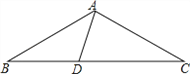
查看答案和解析>>【题目】(10分)如图,在△ABC中,AB=AC,D为BC上一点,∠B=30°,连接AD.
(1)若∠BAD=45°,求证:△ACD为等腰三角形;
(2)若△ACD为直角三角形,求∠BAD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作与实践:已知长方形纸片ABCD中,AD=3,AB=4.
操作一:如图①,任意画一条线段EF,将纸片沿EF折叠,使点B落到点B′的位置,EB′与CD交于点G.试说明重叠部分△EFG为等腰三角形;
操作二:如图②,将纸片沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点H.求△B′HC的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2010,最少经过几次操作 ( )
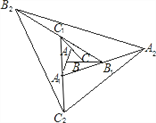
A. 6 B. 5 C. 4 D. 3
相关试题

