【题目】如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2010,最少经过几次操作 ( )
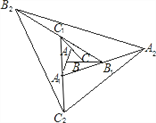
A. 6 B. 5 C. 4 D. 3
参考答案:
【答案】C
【解析】试题分析:先根据已知条件求出△A1B1C1及△A2B2C2的面积,再根据两三角形的倍数关系求解即可.
解:△ABC与△A1BB1底相等(AB=A1B),高为1:2(BB1=2BC),故面积比为1:2,
∵△ABC面积为1,
∴S△A1B1B=2.
同理可得,S△C1B1C=2,S△AA1C=2,
∴S△A1B1C1=S△C1B1C+S△AA1C+S△A1B1B+S△ABC=2+2+2+1=7;
同理可证△A2B2C2的面积=7×△A1B1C1的面积=49,
第三次操作后的面积为7×49=343,
第四次操作后的面积为7×343=2401.
故按此规律,要使得到的三角形的面积超过2015,最少经过4次操作.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索与运用:
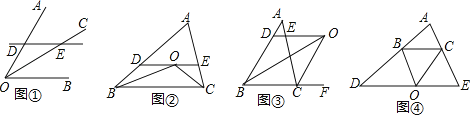
(1)基本图形:如图①,已知OC是∠AOB的角平分线,DE∥OB,分别交OA、OC于点D、E.求证:DE=OD;
(2)在图②中找出这样的基本图形,并利用(1)中的规律解决这个问题:已知△ABC中,两个内角∠ABC与∠ACB的平分线交于点O,过点O作DE∥BC,交AB、AC于点D、E.求证:DE=BD+CE;
(3)若将图②中两个内角的角平分线改为一个内角(如图③,∠ABC)、一个外角(∠ACF)和两个都是外角(如图④∠DBC、∠BCE)的角平分线,其它条件不变,则线段DE、BD、CE的数量关系分别是:图③为 、图④为 :并从中任选一个结论证明.
-
科目: 来源: 题型:
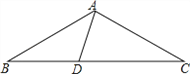
查看答案和解析>>【题目】(10分)如图,在△ABC中,AB=AC,D为BC上一点,∠B=30°,连接AD.
(1)若∠BAD=45°,求证:△ACD为等腰三角形;
(2)若△ACD为直角三角形,求∠BAD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作与实践:已知长方形纸片ABCD中,AD=3,AB=4.
操作一:如图①,任意画一条线段EF,将纸片沿EF折叠,使点B落到点B′的位置,EB′与CD交于点G.试说明重叠部分△EFG为等腰三角形;
操作二:如图②,将纸片沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点H.求△B′HC的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把面值20元的纸币换成1元和5元的两种纸币,则共有_______________种换法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a+b=3,ab=1,则a2+b2=____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠B=∠C,与△ABC全等的△DEF中有一个角是100°,那么在△ABC中与这个100°角对应相等的角是____
相关试题

