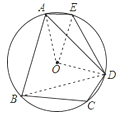
【题目】如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在弧![]() 上.
上.
(1)求∠E的度数;
(2)连接OD、OE,当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,求n的值

参考答案:
【答案】(1)∠AED=120°;(2)12
【解析】试题分析:
(1)如图,连接BD,由已知条件证△ABD是等边三角形,得到∠ABD=60°,从而由圆内接四边形的性质可得∠AED=120°;
(2)如图,连接OA,由∠ABD=60°,可得∠AOD=120°,结合∠DOE=90°,可得∠AOE=30°,从而可得![]() .
.
试题解析:
(1)如图,连接BD,
∵四边形ABCD是⊙O的内接四边形,
∴∠BAD+∠C=180°,
∵∠C=120°,
∴∠BAD=60°,
∵AB=AD,
∴△ABD是等边三角形,
∴∠ABD=60°,
∵四边形ABDE是⊙O的内接四边形,
∴∠AED+∠ABD=180°,
∴∠AED=120°;
(2)连接OA,
∵∠ABD=60°,
∴∠AOD=2∠ABD=120°,
∵∠DOE=90°,
∴∠AOE=∠AOD﹣∠DOE=30°,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请阅读下列材料:
问题:现有
 个边长为
个边长为 的正方形,排列形式如图
的正方形,排列形式如图 ,在图中画出分割线,拼出如图
,在图中画出分割线,拼出如图 所示的新正方形.
所示的新正方形.
请你参考.上述做法,解决如下问题:
(1)现有
 个边长为
个边长为 的正方形,排列形式如图
的正方形,排列形式如图 ,请把它们分割后拼接成一个新的正方形,在图
,请把它们分割后拼接成一个新的正方形,在图 中画出分割线,并在图
中画出分割线,并在图 的正方形网格中用实线画出拼接成的新正方形;(图中每个小正方形的边长均为
的正方形网格中用实线画出拼接成的新正方形;(图中每个小正方形的边长均为 )
)(2)如图
 ,现有由
,现有由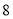 个相同小正方形组成的十字形纸板,请在图中画出分割线,拼出一个新正方形.
个相同小正方形组成的十字形纸板,请在图中画出分割线,拼出一个新正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小亮想了解一根弹簧的长度是如何随所挂物体质量的变化而变化的,他把这根弹簧的上端固定,在其下端悬挂物体.下面是小亮测得的弹簧的长度y与所挂物体质量x的几组对应值.
所挂质量x/kg
0
1
2
3
4
5
弹簧长度y/cm
30
32
34
36
38
40
(1)上表所反映的变化过程中的两个变量,________是自变量,________是因变量;
(2)直接写y与x的关系式;
(3)当弹簧长度为130cm(在弹簧承受范围内)时,求所挂重物的质量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知:
 为等边三角形,点E为射线AC上一点,点D为射线CB上一点,
为等边三角形,点E为射线AC上一点,点D为射线CB上一点, .
.(1)如图1,当E在AC的延长线上且
 时,AD是
时,AD是 的中线吗?请说明理由;
的中线吗?请说明理由;(2)如图2,当E在AC的延长线上时,
 等于AE吗?请说明理由;
等于AE吗?请说明理由;(3)如图3,当D在线段CB的延长线上,E在线段AC上时,请直接写出AB、BD、AE的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在数学课中学习了《解直角三角形》的内容后,双休日组织教学兴趣小组的小伙伴进行实地测量.如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据
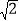 ≈1.41,
≈1.41,  ≈1.73供选用,结果保留整数)
≈1.73供选用,结果保留整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公交车每天的支出费用为600元,每天的乘车人数x(人)与每天利润(利润=票款收入﹣支出费用)y(元)的变化关系如下表所示(每位乘客的乘车票价固定不变):
x(人)
…
200
250
300
350
400
…
Y(元)
…
﹣200
﹣100
0
100
200
…
根据表格中的数据,回答下列问题:
(1)在这个变化关系中,自变量是什么?因变量是什么?
(2)若要不亏本,该公交车每天乘客人数至少达到多少?
(3)请你判断一天乘客人数为500人时,利润是多少?
(4)试写出该公交车每天利润y(元)与每天乘车人数x(人)的关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD⊥AB,垂足为D,E是AC边上一点,EH⊥AB,垂足为H,∠1=∠2.
(1)试说明DF∥AC;
(2)若∠A=38°,∠BCD=45°,求∠3的度数.

相关试题

