【题目】(阅读材料)
小明同学遇到下列问题:
解方程组 ,他发现如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错.如果把方程组中的(2x+3y)看作一个数,把(2x﹣3y)看作一个数,通过换元,可以解决问题.以下是他的解题过程:
,他发现如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错.如果把方程组中的(2x+3y)看作一个数,把(2x﹣3y)看作一个数,通过换元,可以解决问题.以下是他的解题过程:
令m=2x+3y,n=2x﹣3y,
这时原方程组化为 ,解得
,解得![]() ,
,
把![]() 代入m=2x+3y,n=2x﹣3y.
代入m=2x+3y,n=2x﹣3y.
得![]() 解得
解得![]() .
.
所以,原方程组的解为![]()
(解决问题)
请你参考小明同学的做法,解决下面的问题:
(1)解方程组 ;
;
(2)已知方程组![]() 的解是
的解是![]() ,求方程组
,求方程组![]() 的解.
的解.
参考答案:
【答案】(1)原方程组的解为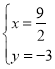 ;(2)
;(2)![]() .
.
【解析】
理解题目中给定的整体代换的思路,按照题目中所给的方法求解方程即可.
(1)令m=![]() ,n=
,n=![]() ,
,
原方程组可化为![]() ,
,
解得:![]() ,
,
∴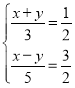 ,
,
解得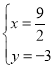
∴原方程组的解为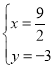 ;
;
(2)令e=x+1,f=﹣y,
原方程组可化为![]() ,
,
依题意,得![]() ,
,
∴![]() ,
,
解得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,
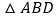 和
和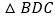 都是边长为1的等边三角形.
都是边长为1的等边三角形.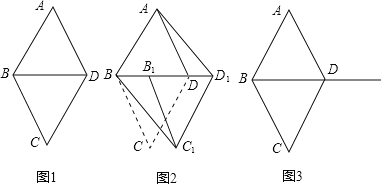
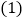 四边形ABCD是菱形吗?为什么?
四边形ABCD是菱形吗?为什么? 如图2,将
如图2,将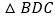 沿射线BD方向平移到
沿射线BD方向平移到 的位置,则四边形
的位置,则四边形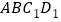 是平行四边形吗?为什么?
是平行四边形吗?为什么?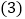 在
在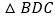 移动过程中,四边形
移动过程中,四边形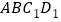 有可能是矩形吗?如果是,请求出点B移动的距离
有可能是矩形吗?如果是,请求出点B移动的距离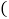 写出过程
写出过程 ;如果不是,请说明理由
;如果不是,请说明理由 图3供操作时使用
图3供操作时使用 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校组织教师为地震救灾捐款,分6个工会小组进行统计,其中第6工会小组尚未统计在内,如图:
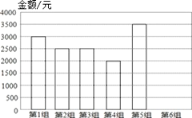
(1)求前5个工会小组捐款金额的众数、中位数和平均数;
(2)若全部6个小组的捐款平均数为2750元,求第6小组的捐款金额,并补全统计图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有大小两种货车,已知1辆大货车与3辆小货车一次可以运货14吨,2辆大货车与5辆小货车一次可以运货25吨.
(1)1辆大货车与1辆小货车一次可以运货各多少吨?
(2)1辆大货车一次费用为300元,1辆小货车一次费用为200元,要求两种货车共用10辆,两次完成80吨的运货任务,且总费用不超过5400元,有哪几种用车方案?请指出费用最低的一种方案,并求出相应的费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a,b)在双曲线y=
 上,若a、b都是正整数,则图象经过B(a,0)、C(0,b)两点的一次函数的解析式(也称关系式)为 .
上,若a、b都是正整数,则图象经过B(a,0)、C(0,b)两点的一次函数的解析式(也称关系式)为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解九年级学生的视力情况,随机抽样调查了部分九年级学生的视力,以下是根据调查结果绘制的统计图表的一部分.
分组
视力
人数
A
3.95≤x≤4.25
3
B
4.25<x≤4.55
C
4.55<x≤4.85
18
D
4.85<x≤5.15
8
E
5.15<x≤5.45
根据以上信息,解谷下列问题:
(1)在被调查学生中,视力在3.95≤x≤4.25范围内的人数为 人;
(2)本次调查的样本容量是 ,视力在5.15<x≤5.45范围内学生数占被调查学生数的百分比是 %;
(3)在统计图中,C组对应扇形的圆心角度数为 °;
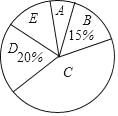
(4)若该校九年级有400名学生,估计视力超过4.85的学生数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
(1)有理化因式:两个含有根式的非零代数式相乘,如果它们的积不含有根式,那么这两个代数式相互叫做有理化因式.例如:
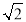 的有理化因式是
的有理化因式是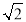 ;
;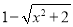 的有理化因式是
的有理化因式是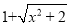 .
.(2)分母有理化:分母有理化又称“有理化分母”,也就是把分母中的根号化去.指的是如果代数式中分母有根号,那么通常将分子、分母同乘以分母的有理化因式,达到去分母中根号的目的.如:
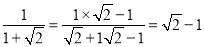 ,
,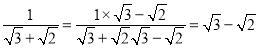
问题解决:
(1)填空:
 的有理化因式是______.(x≥1)
的有理化因式是______.(x≥1)(2)直接写出下列各式分母有理化的结果:
①
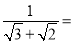 _____;②
_____;②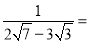 ______.
______.(3)计算:
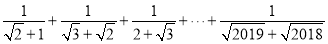 .
.
相关试题

