【题目】阅读理解:
(1)有理化因式:两个含有根式的非零代数式相乘,如果它们的积不含有根式,那么这两个代数式相互叫做有理化因式.例如:![]() 的有理化因式是
的有理化因式是![]() ;
;![]() 的有理化因式是
的有理化因式是![]() .
.
(2)分母有理化:分母有理化又称“有理化分母”,也就是把分母中的根号化去.指的是如果代数式中分母有根号,那么通常将分子、分母同乘以分母的有理化因式,达到去分母中根号的目的.如:![]() ,
,![]()
问题解决:
(1)填空:![]() 的有理化因式是______.(x≥1)
的有理化因式是______.(x≥1)
(2)直接写出下列各式分母有理化的结果:
①![]() _____;②
_____;②![]() ______.
______.
(3)计算:![]() .
.
参考答案:
【答案】(1)![]() ;(2)①
;(2)①![]() ②
②![]() ;(3)
;(3)![]()
【解析】
(1)根据![]() 可得答案;
可得答案;
(2)①分子分母同乘![]() ,再化简即可;
,再化简即可;
②分子分母同乘![]() ,再化简即可;
,再化简即可;
(3)利用分母有理化将式子化简后计算即可.
(1)∵![]()
∴![]() 的有理化因式是
的有理化因式是![]()
故答案为:![]()
(2)①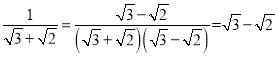
②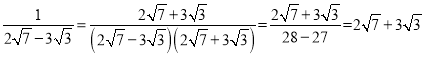
故答案为:①![]() ,②
,②![]() ;
;
(3)![]()
![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读材料)
小明同学遇到下列问题:
解方程组
 ,他发现如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错.如果把方程组中的(2x+3y)看作一个数,把(2x﹣3y)看作一个数,通过换元,可以解决问题.以下是他的解题过程:
,他发现如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错.如果把方程组中的(2x+3y)看作一个数,把(2x﹣3y)看作一个数,通过换元,可以解决问题.以下是他的解题过程:令m=2x+3y,n=2x﹣3y,
这时原方程组化为
 ,解得
,解得 ,
,把
 代入m=2x+3y,n=2x﹣3y.
代入m=2x+3y,n=2x﹣3y.得
 解得
解得 .
.所以,原方程组的解为

(解决问题)
请你参考小明同学的做法,解决下面的问题:
(1)解方程组
 ;
;(2)已知方程组
 的解是
的解是 ,求方程组
,求方程组 的解.
的解. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a,b)在双曲线y=
 上,若a、b都是正整数,则图象经过B(a,0)、C(0,b)两点的一次函数的解析式(也称关系式)为 .
上,若a、b都是正整数,则图象经过B(a,0)、C(0,b)两点的一次函数的解析式(也称关系式)为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解九年级学生的视力情况,随机抽样调查了部分九年级学生的视力,以下是根据调查结果绘制的统计图表的一部分.
分组
视力
人数
A
3.95≤x≤4.25
3
B
4.25<x≤4.55
C
4.55<x≤4.85
18
D
4.85<x≤5.15
8
E
5.15<x≤5.45
根据以上信息,解谷下列问题:
(1)在被调查学生中,视力在3.95≤x≤4.25范围内的人数为 人;
(2)本次调查的样本容量是 ,视力在5.15<x≤5.45范围内学生数占被调查学生数的百分比是 %;
(3)在统计图中,C组对应扇形的圆心角度数为 °;
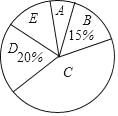
(4)若该校九年级有400名学生,估计视力超过4.85的学生数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的顶点A、B的坐标分别是A(﹣1,0),B(0,﹣2),顶点C、D在双曲线y=
 上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= .
上,边AD交y轴于点E,且四边形BCDE的面积是△ABE面积的5倍,则k= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴的负半轴、y轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在y轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y=
 (x<0)的图象交AB于点N,S矩形OABC=32,tan∠DOE=
(x<0)的图象交AB于点N,S矩形OABC=32,tan∠DOE=  ,则BN的长为 .
,则BN的长为 . 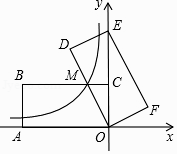
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
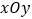 中,已知直线
中,已知直线 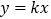 (
(  )分别交反比例函数
)分别交反比例函数 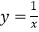 和
和 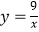 在第一象限的图象于点
在第一象限的图象于点 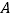 ,
, 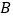 ,过点
,过点 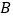 作
作  轴于点
轴于点 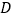 ,交
,交 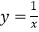 的图象于点
的图象于点 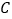 ,连结
,连结 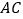 .若
.若 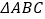 是等腰三角形,则
是等腰三角形,则 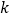 的值是 .
的值是 . 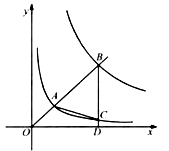
相关试题

