搜索
【题目】如图，在边长为12的正方形ABCD中，E是边CD的中点，将△ADE沿AE对折至△AFE，延长EF交BC于点G．则BG的长为（ ） 
A.5
B.4
C.3
D.2
参考答案：
【答案】B
【解析】解：在正方形ABCD中，AD=AB=BC=CD，∠D=∠B=∠BCD=90°， ∵将△ADE沿AE对折至△AFE，
∴AD=AF，DE=EF，∠D=∠AFE=90°，
∴AB=AF，∠B=∠AFG=90°，
又∵AG=AG，
在Rt△ABG和Rt△AFG中，
，
∴Rt△ABG≌Rt△AFG（HL），
∴BG=GF，
∵E是边CD的中点，
∴DE=CE=6，
设BG=x，则CG=12﹣x，GE=x+6，
∵GE2=CG2+CE2
∴（x+6）2=（12﹣x）2+62 ，
解得 x=4
∴BG=4．
故选B．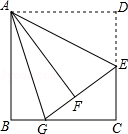
利用翻折变换对应边关系得出AB=AF，∠B=∠AFG=90°，利用HL定理得出△ABG≌△AFG即可；利用勾股定理得出GE2=CG2+CE2 ， 进而求出BG即可；
-
科目： 来源： 题型：
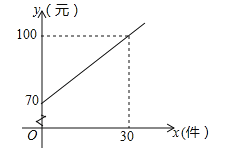
查看答案和解析>>【题目】某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系，如图所示．
（1）求每位“快递小哥”的日收入y（元）与日派送量x（件）之间的函数关系式；
（2）已知某“快递小哥”的日收入不少于110元，则他至少要派送多少件？
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下列材料，并解决有关问题：
我们知道，
，现在我们可以用这一结论来化简含有绝对值的式子，例如化简式子
时，可令
和
，分别求得
，
（称
、
分别为
与
的零点值）。在有理数范围内，零点值和可将全体有理数不重复且不遗漏地分成如下三种情况：（1）
；（2）≤
；（3）
≥2。从而化简代数式可分为以下3种情况：（1）当
时，原式
；（2）当
≤时，原式
；（3）当
≥2时，原式
综上所述：原式
通过以上阅读，请你类比解决以下问题：
（1）填空：
与
的零点值分别为 ；（2）化简式子
。 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线经过A（﹣2，0）B（﹣3，3）及原点O，顶点为C．
（1）求抛物线的解析式；
（2）若点E在抛物线的对称轴上，且A、O、D、E为顶点是四边形是平行四边形，求点D的坐标．
（3）P是抛物线上的第一象限内的动点，过点P作PM⊥x轴，垂足为M，是否存在点P，使得以P、M、A为顶点的三角形△BOC相似？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，数轴上有A、B、C三个点，它们表示的数分别是
、
、
。
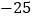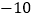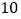（1）填空：AB＝ ，BC＝ ；
（2）现有动点M、N都从A点出发，点M以每秒2个单位长度的速度向右移动，当点M移动到B点时，点N才从A点出发，并以每秒3个单位长度的速度向右移动，求点N移动多少时间，点N追上点M？
（3）若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒3个单位长度和7个单位长度的速度向右运动。试探索：BC－AB的值是否随着时间的变化而改变？请说明理由。
-
科目： 来源： 题型：
查看答案和解析>>【题目】一只小球落在数轴上的某点
，第一次从向左跳1个单位到
，第二次从向右跳2个单位到
，第三次从向左跳3个单位到
，第四次从向右跳4个单位到
，若小球从原点出发，按以上规律跳了6次时，它落在数轴上的点
所表示的数是__________；若小球按以上规律跳了2n次时，它落在数轴上的点
所表示的数恰好是
，则这只小球的初始位置点所表示的数是__________. -
科目： 来源： 题型：
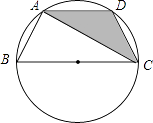
查看答案和解析>>【题目】如图，已知点A、B、C、D均在以BC为直径的圆上，AD∥BC，AC平分∠BCD，∠ADC=120°，四边形ABCD的周长为10，则图中阴影部分的面积为 ．
相关试题
