【题目】阅读下列材料,并解决有关问题:
我们知道, ,现在我们可以用这一结论来化简含有绝对值的式子,例如化简式子
,现在我们可以用这一结论来化简含有绝对值的式子,例如化简式子![]() 时,可令
时,可令![]() 和
和![]() ,分别求得
,分别求得![]() ,
,![]() (称
(称![]() 、
、![]() 分别为
分别为![]() 与
与![]() 的零点值)。在有理数范围内,零点值
的零点值)。在有理数范围内,零点值![]() 和
和![]() 可将全体有理数不重复且不遗漏地分成如下三种情况:(1)
可将全体有理数不重复且不遗漏地分成如下三种情况:(1)![]() ;(2)
;(2)![]() ≤
≤![]() ;(3)
;(3)![]() ≥2。从而化简代数式
≥2。从而化简代数式![]() 可分为以下3种情况:
可分为以下3种情况:
(1)当![]() 时,原式
时,原式![]() ;
;
(2)当![]() ≤
≤![]() 时,原式
时,原式![]() ;
;
(3)当![]() ≥2时,原式
≥2时,原式![]()
综上所述:原式
通过以上阅读,请你类比解决以下问题:
(1)填空:![]() 与
与![]() 的零点值分别为 ;
的零点值分别为 ;
(2)化简式子![]() 。
。
参考答案:
【答案】(1) ![]() 和
和![]() ;(2)
;(2) 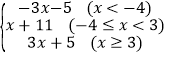
【解析】
(1)令x+2=0和x-4=0,求出x的值即可得出|x+2|和|x-4|的零点值,
(2)零点值x=3和x=-4可将全体实数分成不重复且不遗漏的如下3种情况:x<-4、-4≤x<3和x≥3.分该三种情况找出![]() 的值即可.
的值即可.
解:(1)![]() 和
和![]() ,
,
(2)由![]() 得
得![]() 由
由![]() 得
得![]() ,
,
①当![]() 时,原式
时,原式![]() ,
,
②当![]() ≤
≤![]() 时,原式
时,原式![]() ,
,
③当![]() ≥
≥![]() 时,原式
时,原式![]() ,
,
综上所述:原式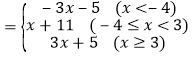 ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】某儿童游乐园门票价格规定如下表:
购票张数
1~50张
51~100张
100张以上
每张票的价格
13元
11元
9元
某校七年级(1)、(2)两个班共102人今年6.1儿童节去游该游乐园,其中(1)班人数较少,不足50人。经估算,如果两个班都以班为单位购票,则一共应付1218元。问:
(1)两个班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可以节省多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,已知线段AB,点C分线段AB为5∶7,点D分线段AB为5∶11,若AB=96cm,求线段CD的长。
(2)如图2,已知线段AB上有C、D两点,AC=
 BC,AD=
BC,AD=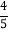 BD,CD=14cm,求线段AB的长。
BD,CD=14cm,求线段AB的长。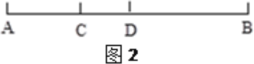
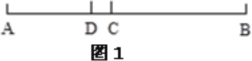
-
科目: 来源: 题型:
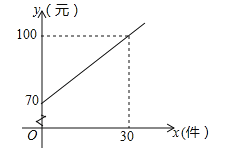
查看答案和解析>>【题目】某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系,如图所示.
(1)求每位“快递小哥”的日收入y(元)与日派送量x(件)之间的函数关系式;
(2)已知某“快递小哥”的日收入不少于110元,则他至少要派送多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过A(﹣2,0)B(﹣3,3)及原点O,顶点为C.

(1)求抛物线的解析式;
(2)若点E在抛物线的对称轴上,且A、O、D、E为顶点是四边形是平行四边形,求点D的坐标.
(3)P是抛物线上的第一象限内的动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形△BOC相似? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为12的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G.则BG的长为( )

A.5
B.4
C.3
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上有A、B、C三个点,它们表示的数分别是
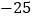 、
、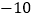 、
、 。
。
(1)填空:AB= ,BC= ;
(2)现有动点M、N都从A点出发,点M以每秒2个单位长度的速度向右移动,当点M移动到B点时,点N才从A点出发,并以每秒3个单位长度的速度向右移动,求点N移动多少时间,点N追上点M?
(3)若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位长度和7个单位长度的速度向右运动。试探索:BC-AB的值是否随着时间的变化而改变?请说明理由。
相关试题

