【题目】如图,数轴上有A、B、C三个点,它们表示的数分别是![]() 、
、![]() 、
、![]() 。
。

(1)填空:AB= ,BC= ;
(2)现有动点M、N都从A点出发,点M以每秒2个单位长度的速度向右移动,当点M移动到B点时,点N才从A点出发,并以每秒3个单位长度的速度向右移动,求点N移动多少时间,点N追上点M?
(3)若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位长度和7个单位长度的速度向右运动。试探索:BC-AB的值是否随着时间的变化而改变?请说明理由。
参考答案:
【答案】(1) AB=15,BC=20;(2) 点N移动15秒时,点N追上点M;(3) BC-AB的值不会随着时间的变化而改变,理由见解析
【解析】
(1)根据数轴上点的位置求出AB与BC的长即可,
(2)不变,理由为:经过t秒后,A、B、C三点所对应的数分别是-24-t,-10+3t,10+7t,表示出BC,AB,求出BC-AB即可做出判断,
(3)经过t秒后,表示P、Q两点所对应的数,根据题意列出关于t的方程,求出方程的解得到t的值,分三种情况考虑,分别求出满足题意t的值即可.
解:(1)AB=15,BC=20,
(2)设点N移动![]() 秒时,点N追上点M,由题意得:
秒时,点N追上点M,由题意得:

![]() ,
,
解得![]() ,
,
答:点N移动15秒时,点N追上点M.
(3)设运动时间是![]() 秒,那么运动后A、B、C三点表示的数分别是
秒,那么运动后A、B、C三点表示的数分别是![]() 、
、![]() 、
、![]() ,
,
∴BC![]() ,AB
,AB![]() ,
,
∴BC-AB![]() ,
,
∴BC-AB的值不会随着时间的变化而改变.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并解决有关问题:
我们知道,
 ,现在我们可以用这一结论来化简含有绝对值的式子,例如化简式子
,现在我们可以用这一结论来化简含有绝对值的式子,例如化简式子 时,可令
时,可令 和
和 ,分别求得
,分别求得 ,
, (称
(称 、
、 分别为
分别为 与
与 的零点值)。在有理数范围内,零点值
的零点值)。在有理数范围内,零点值 和
和 可将全体有理数不重复且不遗漏地分成如下三种情况:(1)
可将全体有理数不重复且不遗漏地分成如下三种情况:(1) ;(2)
;(2) ≤
≤ ;(3)
;(3) ≥2。从而化简代数式
≥2。从而化简代数式 可分为以下3种情况:
可分为以下3种情况:(1)当
 时,原式
时,原式 ;
;(2)当
 ≤
≤ 时,原式
时,原式 ;
;(3)当
 ≥2时,原式
≥2时,原式
综上所述:原式

通过以上阅读,请你类比解决以下问题:
(1)填空:
 与
与 的零点值分别为 ;
的零点值分别为 ;(2)化简式子
 。
。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过A(﹣2,0)B(﹣3,3)及原点O,顶点为C.

(1)求抛物线的解析式;
(2)若点E在抛物线的对称轴上,且A、O、D、E为顶点是四边形是平行四边形,求点D的坐标.
(3)P是抛物线上的第一象限内的动点,过点P作PM⊥x轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形△BOC相似? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为12的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G.则BG的长为( )

A.5
B.4
C.3
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】一只小球落在数轴上的某点
 ,第一次从
,第一次从 向左跳1个单位到
向左跳1个单位到 ,第二次从
,第二次从 向右跳2个单位到
向右跳2个单位到 ,第三次从
,第三次从 向左跳3个单位到
向左跳3个单位到 ,第四次从
,第四次从 向右跳4个单位到
向右跳4个单位到 ,若小球从原点出发,按以上规律跳了6次时,它落在数轴上的点
,若小球从原点出发,按以上规律跳了6次时,它落在数轴上的点 所表示的数是__________;若小球按以上规律跳了2n次时,它落在数轴上的点
所表示的数是__________;若小球按以上规律跳了2n次时,它落在数轴上的点 所表示的数恰好是
所表示的数恰好是 ,则这只小球的初始位置点
,则这只小球的初始位置点 所表示的数是__________.
所表示的数是__________. -
科目: 来源: 题型:
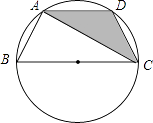
查看答案和解析>>【题目】如图,已知点A、B、C、D均在以BC为直径的圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10,则图中阴影部分的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b2﹣4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b﹣1)x+c<0;其中正确的个数有个.

相关试题

