【题目】如图,已知点A、B、C、D均在以BC为直径的圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10,则图中阴影部分的面积为 . 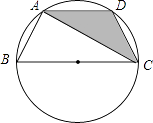
参考答案:
【答案】![]()
【解析】解:设圆心为O,连接OA、OD. ∵AD∥BC,AC平分∠BCD,∠ADC=120°,
∴∠BCD=60°,
∵AC平分∠BCD,
∴∠ACD=30°,
∴∠AOD=2∠ACD=60°,∠OAC=∠ACO=30°.
∴∠BAC=90°,
∴BC是直径,
又∵OA=OD=OB=OC,
则△AOD、△AOB、△COD都是等边三角形.
∴AB=AD=CD.
又∵四边形ABCD的周长为10cm,
∴OB=OC=AB=AD=DC=2(cm).
∴阴影部分的面积=S梯形﹣S△ABC= ![]() (2+4)×
(2+4)× ![]() ﹣
﹣ ![]() ×4×
×4× ![]() =3
=3 ![]() ﹣2
﹣2 ![]() =
= ![]() .
.
故答案为 ![]() .
.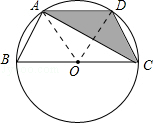
连接OA、OD,则阴影部分的面积等于梯形的面积减去三角形的面积.根据题目中的条件不难发现等边三角形AOD、AOB、COD,从而求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为12的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G.则BG的长为( )

A.5
B.4
C.3
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上有A、B、C三个点,它们表示的数分别是
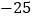 、
、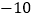 、
、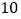 。
。
(1)填空:AB= ,BC= ;
(2)现有动点M、N都从A点出发,点M以每秒2个单位长度的速度向右移动,当点M移动到B点时,点N才从A点出发,并以每秒3个单位长度的速度向右移动,求点N移动多少时间,点N追上点M?
(3)若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位长度和7个单位长度的速度向右运动。试探索:BC-AB的值是否随着时间的变化而改变?请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只小球落在数轴上的某点
 ,第一次从
,第一次从 向左跳1个单位到
向左跳1个单位到 ,第二次从
,第二次从 向右跳2个单位到
向右跳2个单位到 ,第三次从
,第三次从 向左跳3个单位到
向左跳3个单位到 ,第四次从
,第四次从 向右跳4个单位到
向右跳4个单位到 ,若小球从原点出发,按以上规律跳了6次时,它落在数轴上的点
,若小球从原点出发,按以上规律跳了6次时,它落在数轴上的点 所表示的数是__________;若小球按以上规律跳了2n次时,它落在数轴上的点
所表示的数是__________;若小球按以上规律跳了2n次时,它落在数轴上的点 所表示的数恰好是
所表示的数恰好是 ,则这只小球的初始位置点
,则这只小球的初始位置点 所表示的数是__________.
所表示的数是__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=x2+bx+c与y=x的图象如图所示,有以下结论:①b2﹣4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b﹣1)x+c<0;其中正确的个数有个.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将除去零以外的自然数按以下规律排列,根据第一列的奇数行的数的规律,写出第1列第9行的数为______________,再根据第1行的偶数列的规律,写出第3行第6列的数为__________,判断2018所在的位置是第_______行,第_________列.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上三点M,O,N对应的数分别为-1,0,3,点P为数轴上任意一点,其对应的数为x.

(1)MN的长为 ;
(2)如果点P到点M、点N的距离相等,那么x的值是 ;
(3)数轴上是否存在点P,使点P到点M、点N的距离之和是8?若存在,直接写出x的值;若不存在,请说明理由.
(4)如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
相关试题

