【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,四边形
,四边形![]() 为平行四边形,
为平行四边形,![]() 在
在![]() 轴上一定点,
轴上一定点,![]() 为
为![]() 轴上一动点,且点
轴上一动点,且点![]() 从原点
从原点![]() 出发,沿着
出发,沿着![]() 轴正半轴方向以每秒
轴正半轴方向以每秒![]() 个单位长度运动,已知
个单位长度运动,已知![]() 点运动时间为
点运动时间为![]() .
.
(1)点![]() 坐标为________,
坐标为________,![]() 点坐标为________;(直接写出结果,可用
点坐标为________;(直接写出结果,可用![]() 表示)
表示)
(2)当![]() 为何值时,
为何值时,![]() 为等腰三角形;
为等腰三角形;
(3)![]() 点在运动过程中,是否存在
点在运动过程中,是否存在![]() ,使得
,使得![]() ,若存在,请求出
,若存在,请求出![]() 的值,若不存在,请说明理由!
的值,若不存在,请说明理由!

参考答案:
【答案】(1)(4,4),(![]() ,0);(2)1,
,0);(2)1,![]() ,4; (3)存在,
,4; (3)存在,![]()
【解析】
(1)利用平行四边形的性质和根据P点的运动速度,利用路程公式求解即可;
(2)分三种情况:①当![]() 时,②当
时,②当![]() 时,③当
时,③当![]() 时,分别讨论求解,即可得出结果;
时,分别讨论求解,即可得出结果;
(3)过D点作![]() 交BP于点F,设
交BP于点F,设![]() ,则可得
,则可得![]() ,
,![]() ,
,![]() ,利用
,利用![]() ,即可求出
,即可求出![]() 的长,利用路程公式可求得
的长,利用路程公式可求得![]() 的值。
的值。
解:(1)∵![]() ,
,![]() ,四边形
,四边形![]() 为平行四边形,
为平行四边形,
∴点![]() 坐标为(4,4),
坐标为(4,4),
又∵![]() 为
为![]() 轴上一动点,点
轴上一动点,点![]() 从原点
从原点![]() 出发,沿着
出发,沿着![]() 轴正半轴方向以每秒
轴正半轴方向以每秒![]() 个单位长度运动,
个单位长度运动,![]() 点运动时间为
点运动时间为![]() ,
,
∴![]() 点坐标为(
点坐标为(![]() ,0),
,0),
(2)∵B,D的坐标分别为:![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
由勾股定理有:![]() ,
,
当![]() 为等腰三角形时,
为等腰三角形时,
①如图所示,当![]() 时,
时,
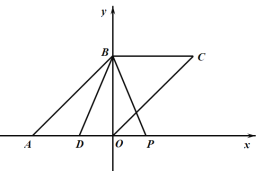
![]() ,
,
∴![]() 点坐标为(
点坐标为(![]() ,0),
,0),
∴![]()
②如图所示,当![]() 时,
时,
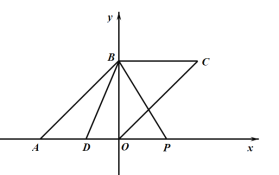
∵![]() ,
,![]()
∴![]() ,
,
∴![]()
③如图所示,当![]() 时,
时,

设P点坐标为:(![]() ,0)
,0)
则有:![]() ,
,![]() ,
,
∴![]() ,解之得:
,解之得:![]()
∴![]() 点坐标为(
点坐标为(![]() ,0),
,0),
∴![]()
综上所述,当![]() 为1,
为1,![]() ,4时,
,4时,![]() 为等腰三角形;
为等腰三角形;
(3)答:存在![]() ,使得
,使得![]() 。
。
证明:∵A,B两点坐标分别为:![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]()
∴![]()
即有:![]() ,
,
如图示,过D点作![]() 交BP于点F,
交BP于点F,

∵![]() ,
,
∴![]() ,
,
设![]() ,根据勾股定理有:
,根据勾股定理有:![]() ,
,
并且![]() ,
,
则:![]()
∴![]() ,
,
化简得:![]() ,
,
解之得:![]() (取正值),
(取正值),
即![]()
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)如图
 ,已知格点(小正方形的顶点):
,已知格点(小正方形的顶点): 、
、 、
、 ,若
,若 为格点,请直接画出所有以
为格点,请直接画出所有以 、
、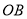 为勾股边且对角线相等的勾股四边形
为勾股边且对角线相等的勾股四边形 ;
;(2)如图
 ,将
,将 绕顶点
绕顶点 按顺时针方向旋转
按顺时针方向旋转 ,得到
,得到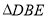 ,连结
,连结 、
、 ,
, ,求证:
,求证: ,即四边形
,即四边形 是勾股四边形;
是勾股四边形;(3)如图
 ,在四边形
,在四边形 中,
中, 为等边三角形,
为等边三角形, ,
, ,
, ,求
,求 长.
长.
-
科目: 来源: 题型:
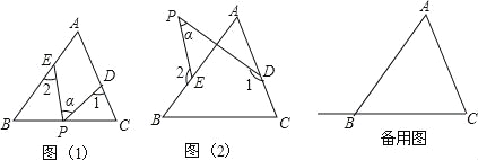
查看答案和解析>>【题目】在△ABC中,∠A=50°,点D,E分别是边AC,AB上的点(不与A,B,C重合),点P是平面内一动点(P与D,E不在同一直线上),设∠PDC=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在边BC上运动(不与点B和点C重合),如图(1)所示,则∠1+∠2=________
(用α的代数式表示).
(2)若点P在ABC的外部,如图(2)所示,则∠α,∠1,∠2之间有何关系?写出你的结论,并说明理由.
(3)当点P在边CB的延长线上运动时,试画出相应图形,标注有关字母与数字,并写出对应的∠α,∠1,∠2之间的关系式.(不需要证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D在△ABC的边BC上,DC=2BD,连接AD与△ABC的中线BE交于点F,连接CF,若△ABC的面积为24,则△AEF的面积为( )

A.4B.5C.6D.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了解九年级学生的身体素质情况,随机抽查了九年级部分学生一分钟跳绳次数,绘制成如下统计图表(图1,图2,表).
等级
一分钟跳绳次数x
人数
A
x>180
12
B
150<x≤180
14
C
120<x≤150
a
D
x≤120
b

请结合图表完成下列问题:
(1)表1中a= ,b= ;
(2)请把图1和图2补充完整;
(3)已知该校有1000名九年级学生,若在一分钟内跳绳次数不大于120次的为不合格,则该校九年级学生一分钟跳绳不合格的学生估计为 人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,CE平分∠BCD与AB交于点E,BF平分∠ABC与AD交于点F,若
 ,EF=4,则CD长为________.
,EF=4,则CD长为________.
-
科目: 来源: 题型:
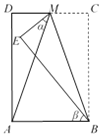
查看答案和解析>>【题目】如图,在长方形ABCD中,点M为CD中点,将△MBC沿BM翻折至△MBE,若∠AME = α,∠ABE = β,则 α 与 β 之间的数量关系为________.
相关试题

