【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)如图![]() ,已知格点(小正方形的顶点):
,已知格点(小正方形的顶点):![]() 、
、![]() 、
、![]() ,若
,若![]() 为格点,请直接画出所有以
为格点,请直接画出所有以![]() 、
、![]() 为勾股边且对角线相等的勾股四边形
为勾股边且对角线相等的勾股四边形![]() ;
;
(2)如图![]() ,将
,将![]() 绕顶点
绕顶点![]() 按顺时针方向旋转
按顺时针方向旋转![]() ,得到
,得到![]() ,连结
,连结![]() 、
、![]() ,
,![]() ,求证:
,求证:![]() ,即四边形
,即四边形![]() 是勾股四边形;
是勾股四边形;
(3)如图![]() ,在四边形
,在四边形![]() 中,
中,![]() 为等边三角形,
为等边三角形,![]() ,
,![]() ,
,![]() ,求
,求![]() 长.
长.

参考答案:
【答案】(1)见解析 (2)见解析 (3)10
【解析】
(1)利用勾股定理计算画出即可.
(2)首先证明△ABC≌△BDC,得出AC=DE,BC=BE,连接CE,进一步得出△BCE为等边三角形;利用等边三角形的性质,进一步得出△DCE是直角三角形,即可解答.
(3)将△ABC逆时针旋转60°,即可得出上△ADE为直角三角形,再根据勾股定理求出ED的值即可解答.
(1)如图1

(2)如图2,连接EC.

根据旋转的性质知△ABC≌△BDC,则BC=BD,AC=DE.
又![]() ∠CBE=60°
∠CBE=60°
![]() △CBE是等边三角形
△CBE是等边三角形
![]() ∠BCE=60°,BD=DE
∠BCE=60°,BD=DE
![]() ∠DCB=30°
∠DCB=30°
![]() ∠BCE+∠DCB=90°即∠DCE=90°
∠BCE+∠DCB=90°即∠DCE=90°
![]()
![]() ,即四边形ABCD是勾股四边形.
,即四边形ABCD是勾股四边形.
(3)如图示,将△ABC逆时针旋转60°,使C,与D点重合,得到△EBD,

则有:AB=AE,AC=ED,∠ABE=60,
∴△ABE为等边三角形,
![]() ∠DAE=∠DAB+∠BAE=30°+60°=90°
∠DAE=∠DAB+∠BAE=30°+60°=90°
![]() △DAE为直角三角形
△DAE为直角三角形
![]()
即:![]()
![]()
故AC=10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MON=ɑ(0°<ɑ<180°),点A.B分别在OM、ON上运动(不与点O重合).
(1)如图1,∠MON=90°,BC是∠ABN的平分线,BC的反方向延长线与∠BAO的平分线交与点D.
①若∠BAO=60°,则∠D=___.
②猜想:∠D的度数是否随A,B的移动发生变化?并说明理由。
(2)如图2,∠MON=α(0°<α<180°)”,∠ABC=
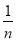 ∠ABN,∠BAD=
∠ABN,∠BAD=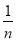 ∠BAO,其余条件不变,则∠D=___°(用含α、n的代数式表示)
∠BAO,其余条件不变,则∠D=___°(用含α、n的代数式表示)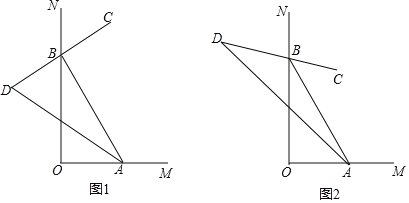
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点B与点D重合,折痕为EF.
(1)求证:BE=BF;
(2)求△ABE的面积;
(3)求折痕EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器商场销售A、B两种型号计算器,两种计算器的进货价格分别为每台30元,40元,商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利润120元.求商场销售A、B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)
-
科目: 来源: 题型:
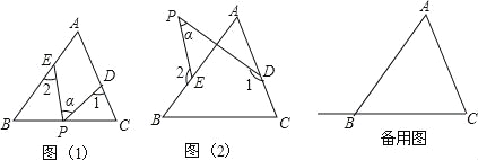
查看答案和解析>>【题目】在△ABC中,∠A=50°,点D,E分别是边AC,AB上的点(不与A,B,C重合),点P是平面内一动点(P与D,E不在同一直线上),设∠PDC=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在边BC上运动(不与点B和点C重合),如图(1)所示,则∠1+∠2=________
(用α的代数式表示).
(2)若点P在ABC的外部,如图(2)所示,则∠α,∠1,∠2之间有何关系?写出你的结论,并说明理由.
(3)当点P在边CB的延长线上运动时,试画出相应图形,标注有关字母与数字,并写出对应的∠α,∠1,∠2之间的关系式.(不需要证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D在△ABC的边BC上,DC=2BD,连接AD与△ABC的中线BE交于点F,连接CF,若△ABC的面积为24,则△AEF的面积为( )

A.4B.5C.6D.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 ,
, ,四边形
,四边形 为平行四边形,
为平行四边形, 在
在 轴上一定点,
轴上一定点, 为
为 轴上一动点,且点
轴上一动点,且点 从原点
从原点 出发,沿着
出发,沿着 轴正半轴方向以每秒
轴正半轴方向以每秒 个单位长度运动,已知
个单位长度运动,已知 点运动时间为
点运动时间为 .
.(1)点
 坐标为________,
坐标为________, 点坐标为________;(直接写出结果,可用
点坐标为________;(直接写出结果,可用 表示)
表示)(2)当
 为何值时,
为何值时, 为等腰三角形;
为等腰三角形;(3)
 点在运动过程中,是否存在
点在运动过程中,是否存在 ,使得
,使得 ,若存在,请求出
,若存在,请求出 的值,若不存在,请说明理由!
的值,若不存在,请说明理由!
相关试题

