【题目】如图,直线![]() 与
与![]() 轴、
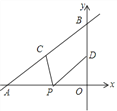
轴、![]() 轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】C
【解析】分析:根据一次函数解析式求出点A、B的坐标,再由中点坐标公式求出点C、D的坐标,根据对称的性质找出点D′的坐标,结合点C、D′的坐标求出直线CD′的解析式,令y=0即可求出x的值,从而得出点P的坐标.
详解:作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时PC+PD值最小,如图所示.
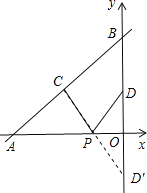
令y=![]() x+4中x=0,则y=4,
x+4中x=0,则y=4,
∴点B的坐标为(0,4);
令y=![]() x+4中y=0,则
x+4中y=0,则![]() x+4=0,解得:x=6,
x+4=0,解得:x=6,
∴点A的坐标为(6,0).
∵点C、D分别为线段AB、OB的中点,
∴点C(3,2),点D(0,2).
∵点D′和点D关于x轴对称,
∴点D′的坐标为(0,2).
设直线CD′的解析式为y=kx+b,
∵直线CD′过点C(3,2),D′(0,2),
∴有![]() ,解得:
,解得: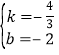 ,
,
∴直线CD′的解析式为y=![]() x2.
x2.
令y=![]() x2中y=0,则0=
x2中y=0,则0=![]() x2,解得:x=
x2,解得:x=![]() ,
,
∴点P的坐标为(![]() ,0).
,0).
故选C.
-
科目: 来源: 题型:
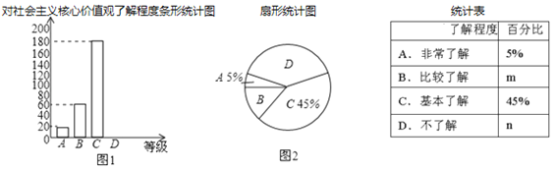
查看答案和解析>>【题目】为了调查学生对社会主义核心价值观的了解程度,我校在学生中做了一次抽样调查,调查结果共分为四个等级:A:非常了解;B:比较了解;C:基本了解;D:不了解.根据调查统计结果,绘制了下面的三种统计图表.
请结合统计图表,回答下列问题.
(1)本次参与调查的学生共有 人,m= ,n= ;
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是 度;
(3)请补全图1所示的条形统计图;
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明是个爱动脑筋的同学,在发现教材中的用方框在月历中移动的规律后,突发奇想,将连续的偶数2、4、6、8,…排成如下表,并用一个十字形框架住其中的五个数,请你仔细观察十字形框架中数字的规律,并回答下列问题:
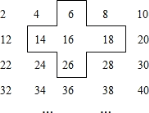
 十字框中的五个数的和与中间的数16有什么关系?
十字框中的五个数的和与中间的数16有什么关系?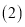 设中间的数为x,用代数式表示十字框中的五个数的和.
设中间的数为x,用代数式表示十字框中的五个数的和. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示.
成绩/
1.50
1.60
1.65
1.70
1.75
1.80
人数
2
3
2
3
4
1
则这些运动员成绩的中位数,众数分别为( )
A. 1.65,1.70 B. 1.65,1.75 C. 1.70,1.75 D. 1.70,1.70
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
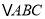 是⊙O的内接三角形,
是⊙O的内接三角形, 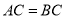 ,
, 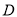 为⊙O中
为⊙O中 上一点,延长
上一点,延长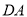 至点
至点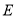 ,使
,使 .
.(1)求证:
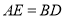 ;
;(2)若
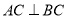 ,求证:AD+BD=
,求证:AD+BD=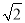 CD.
CD.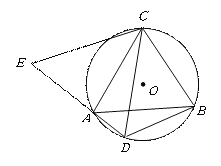
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则菱形ABCD面积为( )
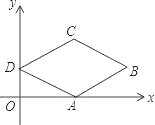
A. 8B. 16C. 24D. 32
-
科目: 来源: 题型:
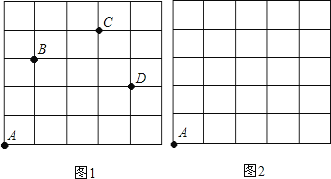
查看答案和解析>>【题目】如图,一只甲虫在5
 5的方格(每一格边长为1)上沿着网格线运动,从A处出发去看望B、C、D处的甲虫,规定:向上向右为正,向下向左为负.例如:从A到B记为:
5的方格(每一格边长为1)上沿着网格线运动,从A处出发去看望B、C、D处的甲虫,规定:向上向右为正,向下向左为负.例如:从A到B记为: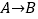 (+1,+3);从C到D 记为:
(+1,+3);从C到D 记为: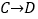 (+1,-2),其中第一个数表示左右方向,第二个数表示上下方向.
(+1,-2),其中第一个数表示左右方向,第二个数表示上下方向.(1)填空:
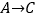 记为( , ),
记为( , ), 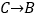 记为( , );
记为( , );(2)若甲虫的行走路线为:
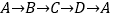 ,请你计算甲虫走过的路程.
,请你计算甲虫走过的路程.(3)若这只甲虫去Q的行走路线依次为:A→M(+2,+2),M→N(+2,-1),N→P(-2,+3),P→Q(-1,-2),请依次在图2标出点M、N、P、Q的位置.
相关试题

