【题目】我们定义:有一组邻角相等且对角线相等的凸四边形叫做“邻对等四边形”.
概念理解
(1)下列四边形中属于邻对等四边形的有 (只填序号);
①顺次连接任意四边形各边中点所得的四边形;
②顺次连接平行四边形各边中点所得的四边形;
③顺次连接矩形各边中点所得的四边形;
④顺次连接菱形各边中点所得的四边形;
性质探究
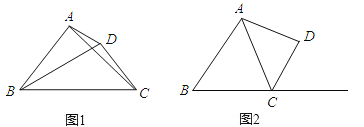
(2)如图1,在邻对等四边形ABCD中,∠ABC=∠DCB,AC=DB,AB>CD,求证:∠BAC与∠CDB互补;
拓展应用
(3)如图2,在四边形ABCD中,∠BCD=2∠B,AC=BC=5,AB=6,CD=4.在BC的延长线上是否存在一点E,使得四边形ABED为邻对等四边形?如果存在,求出DE的长;如果不存在,说明理由.
参考答案:
【答案】(1)④;(2)见解析;(3)存在这样一点E,使得四边形ABED为邻对等四边形,DE=![]()
【解析】
(1)根据中点四边形的特征,结合邻对等四边形的定义求解即可;
(2)延长CD至E,使CE=BA,根据“SAS”可证△ABC≌△ECB,从而BE=CA,∠BAC=∠E.利用等量代换可证BD=BE,从而∠BDE=∠E,然后可证明结论成立;
(3)在BC延长线上取一点E,使得CE=4,连接DE,四边形ABED即为邻对等四边形.连接AE,BD,由等腰三角形的性质和三角形外角的性质可证∠ABC=∠DEB,∠ACE=∠BCD.通过证明CE≌△BCD,可证BD=AE,从而四边形ABED为邻对等四边形.通过证明△ABC∽△DEC,利用相似三角形的性质可求出DE的长.
(1)①顺次连接任意四边形各边中点所得的四边形是平行四边形,平行四边形不具备一组邻角相等且对角线相等,故不是邻对等四边形;
②顺次连接平行四边形各边中点所得的四边形是平行四边形,平行四边形不具备一组邻角相等且对角线相等,故不是邻对等四边形;
③顺次连接矩形各边中点所得的四边形是菱形,菱形不具备一组邻角相等且对角线相等,故不是邻对等四边形;
④顺次连接菱形各边中点所得的四边形是矩形,矩形具备一组邻角相等且对角线相等,故是邻对等四边形;
故答案为④;
(2)∵AB>CD,故可延长CD至E,使CE=BA,
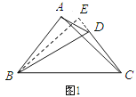
在△ABC与△ECB中,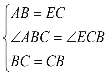 ,
,
∴△ABC≌△ECB.
∴BE=CA,∠BAC=∠E.
∵AC=DB,
∴BD=BE.
∴∠BDE=∠E.
∴∠CDB+∠BDE=∠CDB+∠E=∠BAC+∠CDB=180°.
即∠BAC与∠CDB互补.
(3)存在这样一点E,使得四边形ABED为邻对等四边形,
如图2,在BC延长线上取一点E,使得CE=4,
连接DE,四边形ABED即为邻对等四边形.
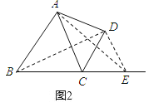
理由如下:
连接AE,BD,
∵CE=CD,
∴∠CDE=∠CED.
∵∠BCD=2∠B,
∴∠ABC=∠DEB,∠ACE=∠BCD.
在△ACE与△BCD中,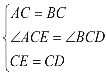 ,
,
∴△ACE≌△BCD.
∴BD=AE,四边形ABED为邻对等四边形.
∵∠CBA=∠CAB=∠CDE=∠CED,
∴△ABC∽△DEC.
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
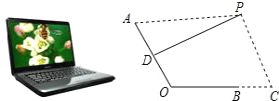
查看答案和解析>>【题目】如图是一台放置在水平桌面上的笔记本电脑,将其侧面抽象成如右图所示的几何图形,若显示屏所在面的侧边AO与键盘所在面的侧边BO长均为24cm,点P为眼睛所在位置,D为AO的中点,连接PD,当PD?AO时,称点P为“最佳视角点”,作PC?BC,垂足C在OB的延长线上,且BC=12cm.
(1)当PA=45cm时,求PC的长;
(2)若?AOC=120°时,“最佳视角点”P在直线PC上的位置会发生什么变化?此时PC的长是多少?请通过计算说明.(结果精确到0.1cm,可用科学计算器,参考数据:
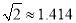 ,
, 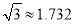 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB是⊙O的直径,AE是弦,OG⊥AE于点G,交⊙O 于点D,连结BD交AE于点F,延长AE至点C,连结BC.
(1)当BC=FC时,证明:BC是⊙O的切线;
(2)已知⊙O的半径
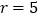 ,当tanA=
,当tanA=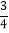 ,求GF的长.
,求GF的长.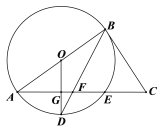
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
 和二次函数
和二次函数 图象的顶点分别为M、N ,与x轴分别相交于A、B两点(点A在点B的左边)和C、D两点(点C在点D的左边),
图象的顶点分别为M、N ,与x轴分别相交于A、B两点(点A在点B的左边)和C、D两点(点C在点D的左边),(1))函数
 的顶点坐标为 ;当二次函数L1 ,L2 的
的顶点坐标为 ;当二次函数L1 ,L2 的 值同时随着
值同时随着 的增大而增大时,
的增大而增大时, 的取值范围是 ;
的取值范围是 ;(2)当AD=MN时,求
 的值,并判断四边形AMDN的形状(直接写出,不必证明);
的值,并判断四边形AMDN的形状(直接写出,不必证明);(3)当B,C是线段AD的三等分点时,求a的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为
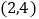 ,点E的坐标为
,点E的坐标为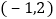 ,则点P的坐标为______.
,则点P的坐标为______.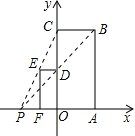
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC是圆O的直径,AB、AD是圆O的弦,且AB=AD,连接BC、DC.
(1)求证:△ABC≌△ADC;
(2)延长AB、DC交于点E,若EC=5 cm,BC=3 cm,求四边形ABCD的面积.

-
科目: 来源: 题型:
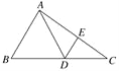
查看答案和解析>>【题目】如图,已知△ABC中,点D在边BC上,∠DAB=∠B,点E在边AC上,满足AE·CD=AD·CE.
(1)求证:DE∥AB;
(2)如果点F是DE延长线上一点,且BD是DF和AB的比例中项,连接AF.求证:DF=AF.
相关试题

