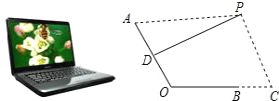
【题目】如图是一台放置在水平桌面上的笔记本电脑,将其侧面抽象成如右图所示的几何图形,若显示屏所在面的侧边AO与键盘所在面的侧边BO长均为24cm,点P为眼睛所在位置,D为AO的中点,连接PD,当PD?AO时,称点P为“最佳视角点”,作PC?BC,垂足C在OB的延长线上,且BC=12cm.
(1)当PA=45cm时,求PC的长;
(2)若?AOC=120°时,“最佳视角点”P在直线PC上的位置会发生什么变化?此时PC的长是多少?请通过计算说明.(结果精确到0.1cm,可用科学计算器,参考数据: ![]() ,
, ![]() )
)
参考答案:
【答案】(1)27cm;(2)位置上升了.34.7cm.
【解析】试题分析:(1)连结PO.先由线段垂直平分线的性质得出PO=PA=45cm,则OC=OB+BC=12+24=36cm,然后利用勾股定理即可求出PC=![]() =27cm;(2)过D作DE⊥OC交BO延长线于E,过D作DF⊥PC于F,则四边形DECF是矩形.先解Rt△DOE,求出DE=DOsin60°=6
=27cm;(2)过D作DE⊥OC交BO延长线于E,过D作DF⊥PC于F,则四边形DECF是矩形.先解Rt△DOE,求出DE=DOsin60°=6![]() ,EO=
,EO=![]() DO=6,则FC=DE=6
DO=6,则FC=DE=6![]() ,DF=EC=EO+OB+BC=42.再解Rt△PDF,求出PF=DFtan30°=42×
,DF=EC=EO+OB+BC=42.再解Rt△PDF,求出PF=DFtan30°=42×![]() =14
=14![]() ,则PC=PF+FC=14
,则PC=PF+FC=14![]() +6
+6![]() =20
=20![]() ≈34.68>27,即可得出结论.
≈34.68>27,即可得出结论.
试题解析:(1)当PA=45cm时,连结PO.如图:
 ∵D为AO的中点,PD⊥AO,∴PO=PA=45cm.∵BO=24cm,BC=12cm,∠C=90°,∴OC=OB+BC=36cm,PC=
∵D为AO的中点,PD⊥AO,∴PO=PA=45cm.∵BO=24cm,BC=12cm,∠C=90°,∴OC=OB+BC=36cm,PC=![]() =27cm;(2)当∠AOC=120°,过D作DE⊥OC交BO延长线于E,过D作DF⊥PC于F,如图:
=27cm;(2)当∠AOC=120°,过D作DE⊥OC交BO延长线于E,过D作DF⊥PC于F,如图:
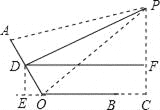 ,则四边形DECF是矩形.在Rt△DOE中,∵∠DOE=60°,DO=
,则四边形DECF是矩形.在Rt△DOE中,∵∠DOE=60°,DO=![]() AO=12,
AO=12,
∴DE=DOsin60°=6![]() ,EO=
,EO=![]() DO=6,∴FC=DE=6
DO=6,∴FC=DE=6![]() ,DF=EC=EO+OB+BC=6+24+12=42.在Rt△PDF中,∵∠PDF=30°,∴PF=DFtan30°=42×
,DF=EC=EO+OB+BC=6+24+12=42.在Rt△PDF中,∵∠PDF=30°,∴PF=DFtan30°=42×![]() =14
=14![]() ,∴PC=PF+FC=14
,∴PC=PF+FC=14![]() +6
+6![]() =20
=20![]() ≈34.68cm>27cm,∴点P在直线PC上的位置上升了.
≈34.68cm>27cm,∴点P在直线PC上的位置上升了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若16﹣xn=(2+x)(2﹣x)(4+x2),则n的值为( )
A.2
B.3
C.4
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C1:y=ax2+4ax+4a+b(a≠0,b>0)的顶点为M,经过原点O且与x轴另一交点为A.
(1)求点A的坐标;
(2)若△AMO为等腰直角三角形,求抛物线C1的解析式;
(3)现将抛物线C1绕着点P(m,0)旋转180°后得到抛物线C2,若抛物线C2的顶点为N,当b=1,且顶点N在抛物线C1上时,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=﹣x2先向下平移2个单位,再向右平移3个单位后所得抛物线的解析式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个等腰三角形两边长之比为1:4,周长为18,则这个等腰三角形底边长为( )
A.2B.6C.8D.2或8
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,结果正确的是( )
A.(a3)2=a6
B.(ab)3=a3b
C.aa3=a3
D.a8÷a4=a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+3的图象与直线y=2x平行,那么此一次函数的表达式为______.
相关试题

