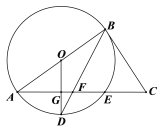
【题目】如图,在⊙O中,AB是⊙O的直径,AE是弦,OG⊥AE于点G,交⊙O 于点D,连结BD交AE于点F,延长AE至点C,连结BC.
(1)当BC=FC时,证明:BC是⊙O的切线;
(2)已知⊙O的半径![]() ,当tanA=
,当tanA=![]() ,求GF的长.
,求GF的长.
参考答案:
【答案】(1)见解析;(2)1
【解析】
(1)由OD⊥AE可知∠D+∠GFD=90°,由等腰三角形的性质可得∠BFC=∠FBC,∠OBD=∠D,从而可证∠OBC=90°;
(2) 连接 BE,在Rt△AOG中,可求出OG= 3, AG=4,由垂径定理得GE= AG=4,然后通过证明△FGD∽△FEB,可求出GF的长.
(1)证明:∵OD⊥AE.
∴∠D+∠GFD=90°.
∵BC=FC,
∴∠BFC=∠FBC.
∵∠BFC=∠GFD,
∴∠GFD=∠FBC.
∵OB=OD,
∴∠OBD=∠D.
∴∠OBD+∠CBF=∠D+∠GFD=90°.
即∠OBC=90°.
∴BC是![]() 的切线.
的切线.
(2) 连接 BE,

∵⊙O半径![]() ,tanA=
,tanA=![]() ,
,
∴sinA=![]() ,cosA=
,cosA=![]() .
.
∴在Rt△AOG中,OG=OA sinA=5×![]() =3, AG=OA cosA=5×
=3, AG=OA cosA=5×![]() =4=GE.
=4=GE.
∴GD=OD-OG=5-3=2.
∵OG⊥AE,
∴AG=GE.
∴OG是△ABE的中位线,
∴BE=2OG=6,BE∥OD.
∴∠D=∠FBE,∠BEF=∠FGD.
∴△FGD∽△FEB.
∴![]() .
.
∴![]() .
.
∴GF=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,等腰Rt△OAB的一条直角边OA 在x轴的正半轴上,点B在双曲线
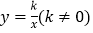 上,且∠BAO=90°,
上,且∠BAO=90°,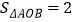 .
.(1)求k的值及点A的坐标;
(2)△OAB沿直线OB平移,当点A恰好在双曲线上时,求平移后点A的对应点A′的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】期末考试后,某市第一中学为了解本校九年级学生期末考试数学学科成绩情况,决定对该年级学生数学学科期末考试成绩进行抽样分析,已知九年级共有12个班,每班48名学生.请按要求回答下列问题:
收集数据
(1)若要从全年级学生中抽取一个96人的样本,你认为以下抽样方法中比较合理的有 .(只要填写序号即可)
①随机抽取两个班级的96名学生;②在全年级学生中随机抽取96名学生;③在全年级12个班中分别各随机抽取8名学生;④从全年级学生中随机抽取96名男生.
整理数据
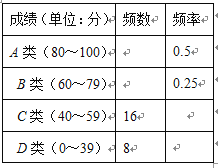
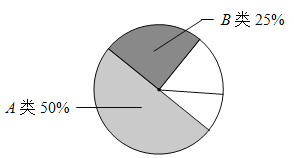
(2)将抽取的96名学生的成绩进行分组,绘制频数分布表和成绩分布扇形统计图(不完整)如下.请根据图表中数据填空:
①C类和D类部分的圆心角度数分别为 、 ;
②估计全年级A、B类学生大约一共有 名.
分析数据
(3)学校为了解其它学校教学情况,将同层次的第一、第二两所中学的抽样数据进行对比,得下表:
学校
平均数(分)
极差(分)
方差
A、B类的频率和
第一中学
71
52
432
0.75
第二中学
71
80
497
0.82
你认为哪所学校的教学效果较好?结合数据,请提出一个合理解释来支持你的观点.
-
科目: 来源: 题型:
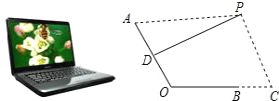
查看答案和解析>>【题目】如图是一台放置在水平桌面上的笔记本电脑,将其侧面抽象成如右图所示的几何图形,若显示屏所在面的侧边AO与键盘所在面的侧边BO长均为24cm,点P为眼睛所在位置,D为AO的中点,连接PD,当PD?AO时,称点P为“最佳视角点”,作PC?BC,垂足C在OB的延长线上,且BC=12cm.
(1)当PA=45cm时,求PC的长;
(2)若?AOC=120°时,“最佳视角点”P在直线PC上的位置会发生什么变化?此时PC的长是多少?请通过计算说明.(结果精确到0.1cm,可用科学计算器,参考数据:
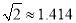 ,
, 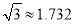 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
 和二次函数
和二次函数 图象的顶点分别为M、N ,与x轴分别相交于A、B两点(点A在点B的左边)和C、D两点(点C在点D的左边),
图象的顶点分别为M、N ,与x轴分别相交于A、B两点(点A在点B的左边)和C、D两点(点C在点D的左边),(1))函数
 的顶点坐标为 ;当二次函数L1 ,L2 的
的顶点坐标为 ;当二次函数L1 ,L2 的 值同时随着
值同时随着 的增大而增大时,
的增大而增大时, 的取值范围是 ;
的取值范围是 ;(2)当AD=MN时,求
 的值,并判断四边形AMDN的形状(直接写出,不必证明);
的值,并判断四边形AMDN的形状(直接写出,不必证明);(3)当B,C是线段AD的三等分点时,求a的值.

-
科目: 来源: 题型:
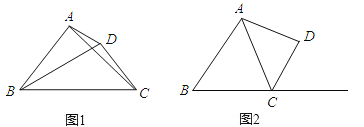
查看答案和解析>>【题目】我们定义:有一组邻角相等且对角线相等的凸四边形叫做“邻对等四边形”.
概念理解
(1)下列四边形中属于邻对等四边形的有 (只填序号);
①顺次连接任意四边形各边中点所得的四边形;
②顺次连接平行四边形各边中点所得的四边形;
③顺次连接矩形各边中点所得的四边形;
④顺次连接菱形各边中点所得的四边形;
性质探究
(2)如图1,在邻对等四边形ABCD中,∠ABC=∠DCB,AC=DB,AB>CD,求证:∠BAC与∠CDB互补;
拓展应用
(3)如图2,在四边形ABCD中,∠BCD=2∠B,AC=BC=5,AB=6,CD=4.在BC的延长线上是否存在一点E,使得四边形ABED为邻对等四边形?如果存在,求出DE的长;如果不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为
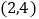 ,点E的坐标为
,点E的坐标为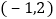 ,则点P的坐标为______.
,则点P的坐标为______.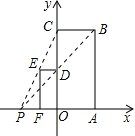
相关试题

