【题目】如图,AC是圆O的直径,AB、AD是圆O的弦,且AB=AD,连接BC、DC.
(1)求证:△ABC≌△ADC;
(2)延长AB、DC交于点E,若EC=5 cm,BC=3 cm,求四边形ABCD的面积.

参考答案:
【答案】(1)见解析;(2)四边形ABCD的面积为18 cm2
【解析】
(1)根据直径所对的圆周角是直角进行证明.
(2)由(1)的结论得到DE、CD长度,再通过∠EAD=∠ECB,∠D=∠EBC=90°,得到△EAD∽△ECB,再通过相似三角形成比例以及勾股定理得到BE、AD的长再进行四边形面积的求解即可.
(1)证明 ∵AC是圆O的直径,
∴∠ABC=∠D=90°,
在Rt△ABC与Rt△ADC中,
![]() ,
,
∴Rt△ABC≌Rt△ADC;
(2)解 由(1)知Rt△ABC≌Rt△ADC,
∴CD=BC=3,AD=AB,
∴DE=5+3=8,
∵∠EAD=∠ECB,∠D=∠EBC=90°,
∴△EAD∽△ECB,
∴![]() =
=![]() ,
,
∵BE=![]() =4,
=4,
∴![]() =
=![]() ,
,
∴AD=6,
∴四边形ABCD的面积=S△ABC+S△ACD=2×![]() ×3×6=18 cm2
×3×6=18 cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
 和二次函数
和二次函数 图象的顶点分别为M、N ,与x轴分别相交于A、B两点(点A在点B的左边)和C、D两点(点C在点D的左边),
图象的顶点分别为M、N ,与x轴分别相交于A、B两点(点A在点B的左边)和C、D两点(点C在点D的左边),(1))函数
 的顶点坐标为 ;当二次函数L1 ,L2 的
的顶点坐标为 ;当二次函数L1 ,L2 的 值同时随着
值同时随着 的增大而增大时,
的增大而增大时, 的取值范围是 ;
的取值范围是 ;(2)当AD=MN时,求
 的值,并判断四边形AMDN的形状(直接写出,不必证明);
的值,并判断四边形AMDN的形状(直接写出,不必证明);(3)当B,C是线段AD的三等分点时,求a的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们定义:有一组邻角相等且对角线相等的凸四边形叫做“邻对等四边形”.
概念理解
(1)下列四边形中属于邻对等四边形的有 (只填序号);
①顺次连接任意四边形各边中点所得的四边形;
②顺次连接平行四边形各边中点所得的四边形;
③顺次连接矩形各边中点所得的四边形;
④顺次连接菱形各边中点所得的四边形;
性质探究
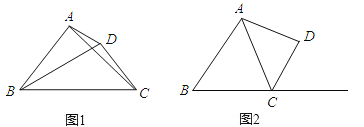
(2)如图1,在邻对等四边形ABCD中,∠ABC=∠DCB,AC=DB,AB>CD,求证:∠BAC与∠CDB互补;
拓展应用
(3)如图2,在四边形ABCD中,∠BCD=2∠B,AC=BC=5,AB=6,CD=4.在BC的延长线上是否存在一点E,使得四边形ABED为邻对等四边形?如果存在,求出DE的长;如果不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为
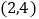 ,点E的坐标为
,点E的坐标为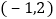 ,则点P的坐标为______.
,则点P的坐标为______.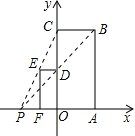
-
科目: 来源: 题型:
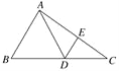
查看答案和解析>>【题目】如图,已知△ABC中,点D在边BC上,∠DAB=∠B,点E在边AC上,满足AE·CD=AD·CE.
(1)求证:DE∥AB;
(2)如果点F是DE延长线上一点,且BD是DF和AB的比例中项,连接AF.求证:DF=AF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的顶点坐标为A(-2,3),B(-3,2),C(-1,1).
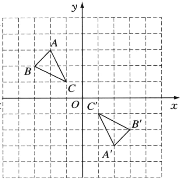
(1)若将△ABC向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的△A1B1C1;
(2)画出△A1B1C1绕原点旋转180°后得到的△A2B2C2;
(3)△A'B'C'与△ABC是位似图形,请写出位似中心的坐标:______;
(4)顺次连接C,C1,C',C2,所得到的图形是轴对称图形吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=
 和y=
和y= 在第一象限内的图象如图,点P是y=
在第一象限内的图象如图,点P是y= 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y=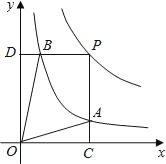 的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=
的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=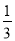 AP.其中所有正确结论的序号是( )
AP.其中所有正确结论的序号是( )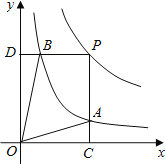
A. ①②③ B. ②③④ C. ①③④ D. ①②④
相关试题

