【题目】已知:如图,在正方形ABCD中,AB=4,点G是射线AB上的一个动点,以DG为边向右作正方形DGEF,作EH⊥AB于点H.
(1)若点G在点B的右边.试探索:EH![]() BG的值是否为定值,若是,请求出定值;若不是,请说明理由.
BG的值是否为定值,若是,请求出定值;若不是,请说明理由.

(2)连接EB,在G点的整个运动(点G与点A重合除外)过程中,求∠EBH的度数.
参考答案:
【答案】(1)EH![]() BG的值是定值4,(2)在G点的整个运动(点G与点A重合除外)过程中,∠EBH都等于45°
BG的值是定值4,(2)在G点的整个运动(点G与点A重合除外)过程中,∠EBH都等于45°
【解析】分析:![]() 根据垂直的定义得到∠GHE=90°,根据余角的性质得到
根据垂直的定义得到∠GHE=90°,根据余角的性质得到![]() 根据正方形的性质得到
根据正方形的性质得到![]() 判断出
判断出![]() 证明
证明![]() ≌
≌![]() ,根据全等三角形的性质得到
,根据全等三角形的性质得到![]() ,根据线段的和差即可得到结论;
,根据线段的和差即可得到结论;
(2)分三种情况讨论:利用(1)得出![]() ≌
≌![]() ,再判断出△BHE是等腰直角三角形,即可得出结论.
,再判断出△BHE是等腰直角三角形,即可得出结论.
详解:(1)![]() 的值是定值,
的值是定值,
![]()
又![]() ,∴
,∴![]()
∵四边形ABCD与四边形DGEF都是正方形,
∴![]() ,∴
,∴![]()
在![]() 和
和![]() 中,
中,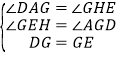 ,
,
∴![]() ≌
≌![]() (AAS);
(AAS);
∴![]()
又AG=AB+BG,AB=4,
∴EH=AB+BG,
∴EHBG=AB=4;
(2)(I)当点G在点B的左侧时,如图1,

同(2)①可证得:△DAG≌△GHE,
∴GH=DA=AB,EH=AG,
∴GB+BH=AG+GB,
∴BH=AG=EH,又![]() ,
,
∴△BHE是等腰直角三角形,
∴![]()
(II)如图2,当点G在点B的右侧时,
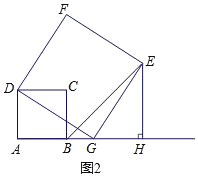
由(2)①证得:△DAG≌△GHE.
∴GH=DA=AB,EH=AG,
∴AB+BG=BG+GH,
∴AG=BH,又EH=AG
∴EH=HB,又![]() ,
,
∴△BHE是等腰直角三角形,
∴![]()
(III)当点G与点B重合时,
如图3,同理可证:△DAG≌△GHE,
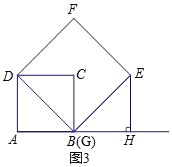
∴GH=DA=AB,EH=AG=AB,
∴△GHE(即△BHE)是等腰直角三角形,
∴![]()
综上,在G点的整个运动(点G与点A重合除外)过程中,∠EBH都等于![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)停车难已成为合肥城市病之一,主要表现在居住停车位不足,停车资源结构性失衡,中心城区供需差距大等等.如图是张老师的车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,已知小汽车车门宽AO为 1.2 米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个角之差的绝对值等于45°,则称这两个角互为“半余角”,即若|∠α-∠β |=45°,则称∠α、∠β互为半余角.(注:本题中的角是指大于0°且小于180°的角)
(1)若∠A=80°,则∠A的半余角的度数为 ;
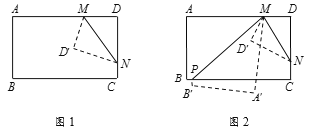
(2)如图1,将一长方形纸片ABCD沿着MN折叠(点M在线段AD上,点N在线段CD上)使点D落在点D′处,若∠AMD′与∠DMN互为“半余角”,求∠DMN的度数;
(3)在(2)的条件下,再将纸片沿着PM折叠(点P在线段BC上),点A、B分别落在点A′、B′处,如图2.若∠AMP比∠DMN大5°,求∠A′MD′的度数.
-
科目: 来源: 题型:
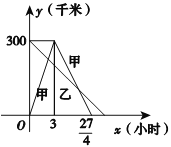
查看答案和解析>>【题目】已知:甲乙两车分别从相距300千米的A,B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
(1)求甲车离出发地的距离y甲(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(2)若已知乙车行驶的速度是40千米/小时,它们在行驶过程中何时相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某加工厂购进甲、乙两种原料,若甲原料的单价为
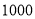 元
元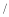 千克,乙原料的单价为
千克,乙原料的单价为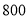 元
元 千克.现该工厂预计用不多于
千克.现该工厂预计用不多于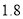 万元且不少于
万元且不少于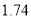 万元的资金购进这两种原料共
万元的资金购进这两种原料共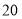 千克.
千克.(l)若需购进甲原料
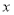 千克,请求出
千克,请求出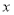 的取值范围;
的取值范围;(2)经加工后:甲原料加工的产品,利润率为
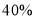 ;每一千克乙原料加工的产品售价为
;每一千克乙原料加工的产品售价为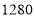 元.则应该怎样安排进货,才能使销售的利润最大?
元.则应该怎样安排进货,才能使销售的利润最大?(3)在(2)的条件下,为了促销,公司决定每售出一千克乙原料加工的产品,返还顾客现金
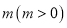 元,而甲原料加工的产品售价不变,要使所有进货方案获利相同,求
元,而甲原料加工的产品售价不变,要使所有进货方案获利相同,求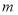 的值
的值 -
科目: 来源: 题型:
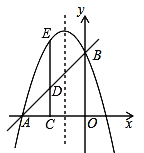
查看答案和解析>>【题目】已知直线y=x+3交x轴于点A,交y轴于点B,抛物线y=
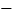 x2+bx+c经过点A,B.
x2+bx+c经过点A,B.(1)求抛物线解析式;
(2)点C(m,0)在线段OA上(点C不与A,O点重合),CD⊥OA交AB于点D,交抛物线于点E,若DE=
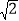 AD,求m的值;
AD,求m的值;(3)点M在抛物线上,点N在抛物线的对称轴上,在(2)的条件下,是否存在以点D,B,M,N为顶点的四边形为平行四边形?若存在,请求出点N的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是学校的大门,教师的办公室A位于点O的北偏东45°,学生宿舍B位于点O的南偏东30°,
(1)请在图中画出射线OA、射线OB,并计算∠AOB的度数;
(2)七年级教室C在∠AOB的角平分线上,画出射线OC,并通过计算说明七年级教室相对于点O的方位角.
相关试题

