【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y= ![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y= ![]() 的图象上,则k的值为( )
的图象上,则k的值为( ) 
A.﹣4
B.4
C.﹣2
D.2
参考答案:
【答案】A
【解析】解:过点A,B作AC⊥x轴,BD⊥x轴,分别于C,D.
设点A的坐标是(m,n),则AC=n,OC=m,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∵∠DBO+∠BOD=90°,
∴∠DBO=∠AOC,
∵∠BDO=∠ACO=90°,
∴△BDO∽△OCA,
∴ ![]() =
= ![]() =
= ![]() ,
,
∵OB=2OA,
∴BD=2m,OD=2n,
因为点A在反比例函数y= ![]() 的图象上,则mn=1,
的图象上,则mn=1,
∵点B在反比例函数y= ![]() 的图象上,B点的坐标是(﹣2n,2m),
的图象上,B点的坐标是(﹣2n,2m),
∴k=﹣2n2m=﹣4mn=﹣4.
故选A.
要求函数的解析式只要求出B点的坐标就可以,过点A,B作AC⊥x轴,BD⊥x轴,分别于C,D.根据条件得到△ACO∽△ODB,得到: ![]() =
= ![]() =
= ![]() =2,然后用待定系数法即可.
=2,然后用待定系数法即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知双曲线y=
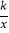 (k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,4),则△AOC的面积为( )
(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,4),则△AOC的面积为( )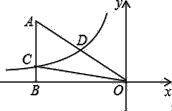
A. 6 B. 12 C. 18 D. 24
-
科目: 来源: 题型:
查看答案和解析>>【题目】正六边形的边心距为
 ,这个正六边形的面积为( )
,这个正六边形的面积为( )
A.2
B.4
C.6
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B、C、D在同一条直线上,点E、F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
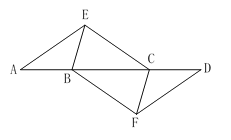
(1)求证:△ACE≌△DBF;
(2)求证:四边形BFCE是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣3,﹣1,0,1,3这五个数中随机抽取一个数记为a,再从剩下的四个数中任意抽取一个数记为b,恰好使关于x,y的二元一次方程组
 有整数解,且点(a,b)落在双曲线
有整数解,且点(a,b)落在双曲线 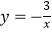 上的概率是 .
上的概率是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(2
 ,2)、B(2
,2)、B(2  ,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(﹣2
,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(﹣2  ,2
,2  )的位置,则图中阴影部分的面积为 .
)的位置,则图中阴影部分的面积为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若四边形ABCD、四边形GFED都是正方形,AD=4,
 ,当正方形GFED绕D旋转到如图的位置,点F在边AD上,延长CE交AG于H,交AD于M.则CM的长为 .
,当正方形GFED绕D旋转到如图的位置,点F在边AD上,延长CE交AG于H,交AD于M.则CM的长为 . 
相关试题

