【题目】如图,已知A(2 ![]() ,2)、B(2
,2)、B(2 ![]() ,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(﹣2
,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(﹣2 ![]() ,2
,2 ![]() )的位置,则图中阴影部分的面积为 .
)的位置,则图中阴影部分的面积为 . 
参考答案:
【答案】![]() π
π
【解析】解:∵A(2 ![]() ,2)、A′(﹣2
,2)、A′(﹣2 ![]() ,2
,2 ![]() ),
),
∴∠A′OA=45°+60°=105°,
∵将△AOB绕着点O逆时针旋转,使点A(2 ![]() ,2)旋转到点A′(﹣2,2
,2)旋转到点A′(﹣2,2 ![]() )的位置,B旋转到点B′位置,
)的位置,B旋转到点B′位置,
∴∠A′OA=∠B′OB=105°,
∵B(2 ![]() ,1),A′(﹣2
,1),A′(﹣2 ![]() ,2
,2 ![]() ),
),
∴B′点坐标为(﹣2 ![]() +1,2
+1,2 ![]() );
);
如图,设 ![]() 交OA′于C′,
交OA′于C′,
∵A(2 ![]() ,2)、B(2
,2)、B(2 ![]() ,1),
,1),
∴OA=4,OC=OB= ![]() .
.
根据旋转的性质可得,S△OB′C′=S△OBC ,
∴阴影部分的面积=S扇形A'OA﹣S扇形C'OC= ![]() ﹣
﹣ ![]() =
= ![]() π,
π,
所以答案是: ![]() π.
π.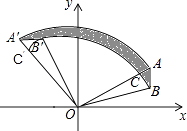
【考点精析】本题主要考查了旋转的性质的相关知识点,需要掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B、C、D在同一条直线上,点E、F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
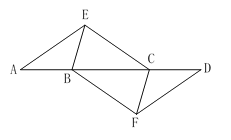
(1)求证:△ACE≌△DBF;
(2)求证:四边形BFCE是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=
 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y=  的图象上,则k的值为( )
的图象上,则k的值为( ) 
A.﹣4
B.4
C.﹣2
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣3,﹣1,0,1,3这五个数中随机抽取一个数记为a,再从剩下的四个数中任意抽取一个数记为b,恰好使关于x,y的二元一次方程组
 有整数解,且点(a,b)落在双曲线
有整数解,且点(a,b)落在双曲线 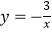 上的概率是 .
上的概率是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若四边形ABCD、四边形GFED都是正方形,AD=4,
 ,当正方形GFED绕D旋转到如图的位置,点F在边AD上,延长CE交AG于H,交AD于M.则CM的长为 .
,当正方形GFED绕D旋转到如图的位置,点F在边AD上,延长CE交AG于H,交AD于M.则CM的长为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点A(a,0),B(0,b),且a、b满足
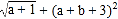 =0, □ABCD的边AD与y轴交于点E(0,2),且E为AD中点,双曲线
=0, □ABCD的边AD与y轴交于点E(0,2),且E为AD中点,双曲线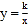 经过C、D两点.
经过C、D两点. (1)求k的值;
(2)点P在双曲线
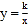 上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;(3)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时,
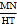 的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.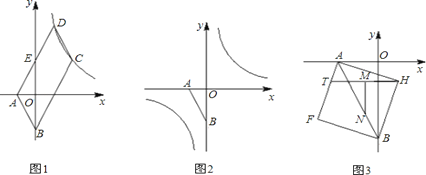
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=k1x+b(k1≠0)与反比例函数
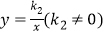 的图象交于点A(-1,2),B(m,-1).
的图象交于点A(-1,2),B(m,-1).(1)求一次函数与反比例函数的解析式;
(2)在x轴上是否存在点P(n,0),使△ABP为等腰三角形,请你直接写出P点的坐标.

相关试题

