【题目】如图,已知双曲线y=![]() (k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,4),则△AOC的面积为( )
(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,4),则△AOC的面积为( )
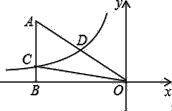
A. 6 B. 12 C. 18 D. 24
参考答案:
【答案】B
【解析】
已知A点坐标![]() ,且D点为直角三角形OAB斜边的中点,由三角形的性质可知点D的坐标,将D点坐标代入反比例函数
,且D点为直角三角形OAB斜边的中点,由三角形的性质可知点D的坐标,将D点坐标代入反比例函数![]() 可以解得k的值,又直角边AB和反比例函数
可以解得k的值,又直角边AB和反比例函数![]() 相交于点C,结合图像和反比例函数可知C点坐标,从而可以求出△OBC的面积,用大三角形OAB减去小三角形OBC的面积求出△AOC的面积.
相交于点C,结合图像和反比例函数可知C点坐标,从而可以求出△OBC的面积,用大三角形OAB减去小三角形OBC的面积求出△AOC的面积.
∵点D是Rt△OAB斜边的中点,且点A坐标![]() ,∴点D坐标
,∴点D坐标![]() ,将点D坐标
,将点D坐标![]() 代入反比例函数
代入反比例函数![]() 中有
中有![]() ,∴反比例函数
,∴反比例函数![]() ∵线段AB与反比例函数
∵线段AB与反比例函数![]() 交于点C结合图像知C点横坐标为-8,代入反比例函数
交于点C结合图像知C点横坐标为-8,代入反比例函数![]() ,∴
,∴![]() ,∴D点坐标为
,∴D点坐标为![]() ,∵△OAB为直角三角形,∴∠ABO=90°,所以S△OAB=
,∵△OAB为直角三角形,∴∠ABO=90°,所以S△OAB=![]() ×8×4=16,S△OBC=
×8×4=16,S△OBC=![]() ×8×1=4,∴S△AOC=S△OAB-S△OBC=16-4=12,故本题答案选择B.
×8×1=4,∴S△AOC=S△OAB-S△OBC=16-4=12,故本题答案选择B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2﹣(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点.

(1)求m的值;
(2)求A、B两点的坐标;
(3)当﹣3<x<1时,在抛物线上是否存在一点P,使得△PAB的面积是△ABC面积的2倍?若存在,请求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为原点,点B在x轴的正半轴上,D(0,8),将矩形OBCD折叠,使得顶点B落在CD边上的P点处.
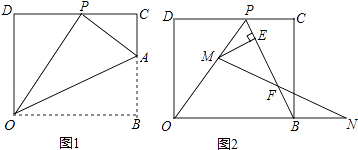
(1)如图①,已知折痕与边BC交于点A,若OD=2CP,求点A的坐标.
(2)若图①中的点 P 恰好是CD边的中点,求∠AOB的度数.
(3)如图②,在(I)的条件下,擦去折痕AO,线段AP,连接BP,动点M在线段OP上(点M与P,O不重合),动点N在线段OB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E,试问当点M,N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度(直接写出结果即可 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△
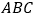 中,
中,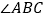 的平分线与
的平分线与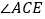 的平分线相交于点
的平分线相交于点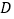 .
.⑴.若
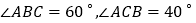 ,求
,求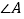 和
和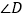 度数;
度数;⑵.由第⑴小题的计算,发现
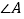 和
和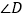 有什么关系?它们是不是一定有这种关系?请作出说明.
有什么关系?它们是不是一定有这种关系?请作出说明.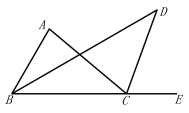
-
科目: 来源: 题型:
查看答案和解析>>【题目】正六边形的边心距为
 ,这个正六边形的面积为( )
,这个正六边形的面积为( )
A.2
B.4
C.6
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B、C、D在同一条直线上,点E、F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
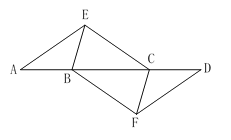
(1)求证:△ACE≌△DBF;
(2)求证:四边形BFCE是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=
 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y=  的图象上,则k的值为( )
的图象上,则k的值为( ) 
A.﹣4
B.4
C.﹣2
D.2
相关试题

