【题目】正六边形的边心距为 ![]() ,这个正六边形的面积为( )
,这个正六边形的面积为( )
A.2 ![]()
B.4 ![]()
C.6 ![]()
D.12
参考答案:
【答案】C
【解析】解:如图,连接OA、OB;过点O作OG⊥AB于点G.
在Rt△AOG中,OG= ![]() ,∠AOG=30°,
,∠AOG=30°,
∵OG=OAcos 30°,
∴OA= ![]() =
= ![]() =2,
=2,
∴这个正六边形的面积=6S△OAB=6× ![]() ×2×
×2× ![]() =6
=6 ![]() .
.
故选C.
【考点精析】解答此题的关键在于理解正多边形的定义的相关知识,掌握在平面内,各个角都相等,各条边都相等的多边形叫做正多边形,以及对正多边形的性质的理解,了解正多边形都是轴对称图形.一个正n边形共有n条对称轴,每条对称轴都通过正n边形的中心;正多边形的中心边数为偶数的正多边形是中心对称图形,它的对称中心是正多边形的中心.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为原点,点B在x轴的正半轴上,D(0,8),将矩形OBCD折叠,使得顶点B落在CD边上的P点处.
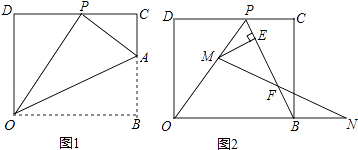
(1)如图①,已知折痕与边BC交于点A,若OD=2CP,求点A的坐标.
(2)若图①中的点 P 恰好是CD边的中点,求∠AOB的度数.
(3)如图②,在(I)的条件下,擦去折痕AO,线段AP,连接BP,动点M在线段OP上(点M与P,O不重合),动点N在线段OB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E,试问当点M,N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度(直接写出结果即可 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△
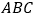 中,
中,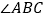 的平分线与
的平分线与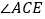 的平分线相交于点
的平分线相交于点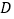 .
.⑴.若
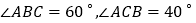 ,求
,求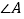 和
和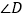 度数;
度数;⑵.由第⑴小题的计算,发现
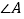 和
和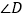 有什么关系?它们是不是一定有这种关系?请作出说明.
有什么关系?它们是不是一定有这种关系?请作出说明.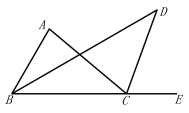
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知双曲线y=
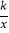 (k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,4),则△AOC的面积为( )
(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,4),则△AOC的面积为( )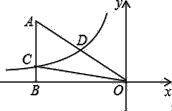
A. 6 B. 12 C. 18 D. 24
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B、C、D在同一条直线上,点E、F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
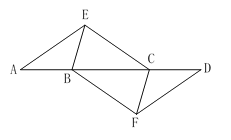
(1)求证:△ACE≌△DBF;
(2)求证:四边形BFCE是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=
 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y=  的图象上,则k的值为( )
的图象上,则k的值为( ) 
A.﹣4
B.4
C.﹣2
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣3,﹣1,0,1,3这五个数中随机抽取一个数记为a,再从剩下的四个数中任意抽取一个数记为b,恰好使关于x,y的二元一次方程组
 有整数解,且点(a,b)落在双曲线
有整数解,且点(a,b)落在双曲线 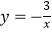 上的概率是 .
上的概率是 .
相关试题

